Излучение электромагнитных волн. Элементарный электрический излучатель. Мощность и сопротивление излучателя, страница 2

Рисунок 6.2

        

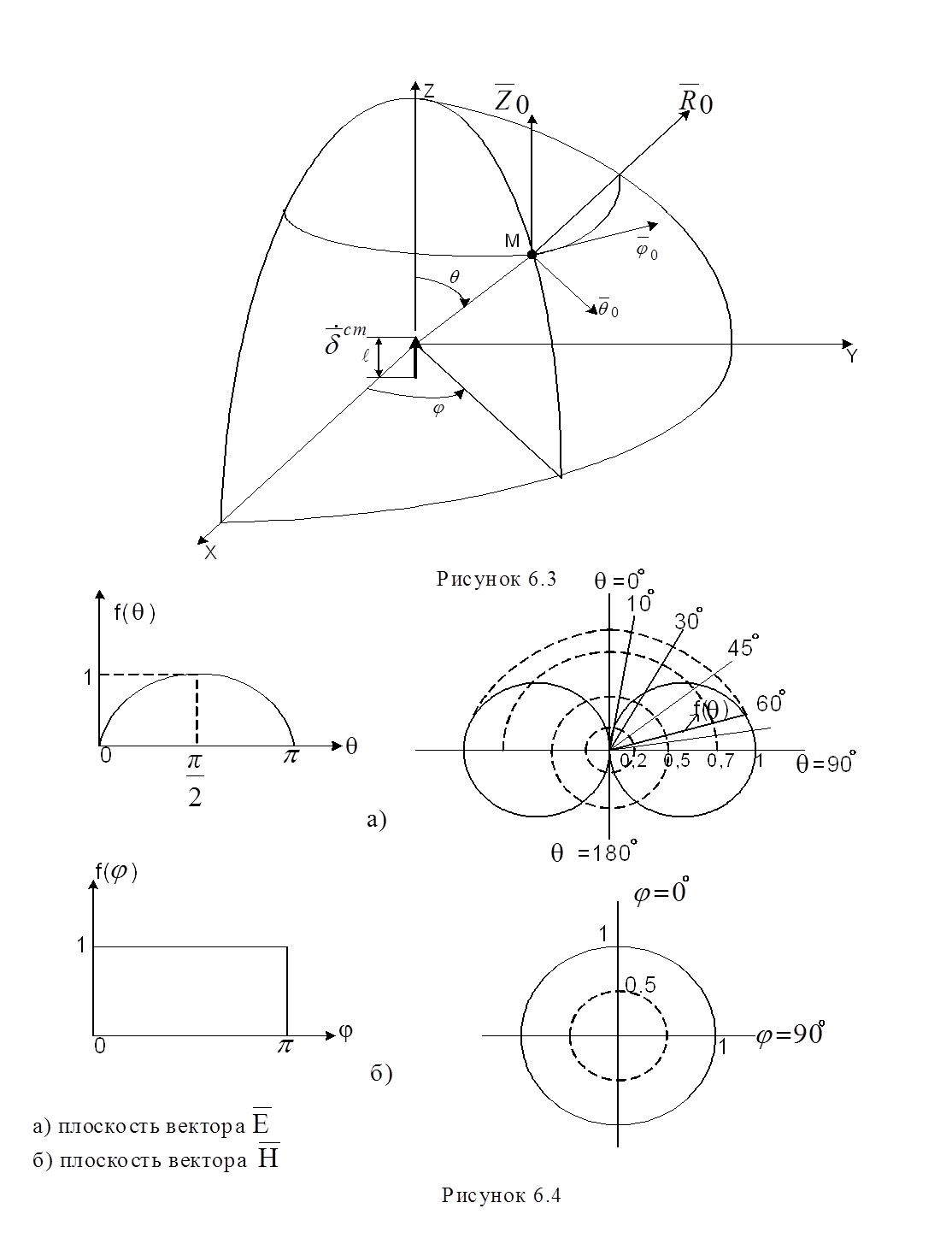
             В ближней и дальней зонах можно использовать более простые, но приближенные формулы.

             Охарактеризуем кратко ближнюю зону. При KR<<1   . Удерживая в (6.1) лишь один член, содержащий 1/KR в высшей степени, получаем:

                                ; ; 

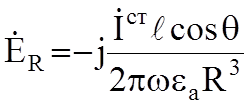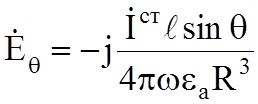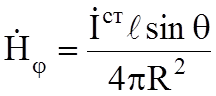                                                                                                      (6.2)

ЭМП в ближней зоне практически не имеет сдвига по фазе по координате R, значит нет бегущей волны, векторы и ,  сдвинуты на угол p/2. Это значит, что средне значение вектора Пойтинга , переноса энергии нет, нет излучения из ближней зоны. Энергия Т/4 периода двигается от излучателя, Т/4 в обратном направлении – к излучателю. Происходит обмен энергией между излучателем и ближней зоной, - колебательный режим. В ближней зоне сосредоточена реактивная энергия излучателя. На практике стремятся уменьшить размеры ближней зоны, для организации радиосвязи ее нельзя использовать.

             Рассмотрим дальнюю или волновую зону, в которой KR>>1. Удерживая в (6.1) члены содержащие 1/KR в низшей степени получим:

                              ; 

                              ,

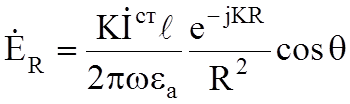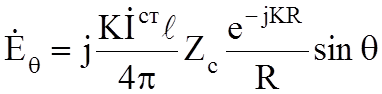
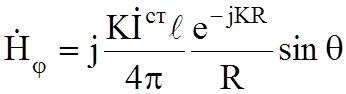             где .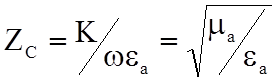

             Составляющая в KR раз меньше, чем   и в дальней зоне ею можно пренебречь. Перейдем к мгновенным значениям:

                                 ;

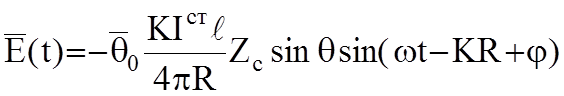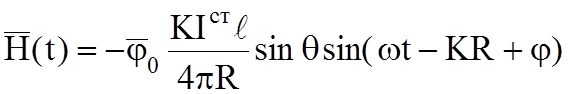                                                      (6.3)

             В дальней зоне ЭМВ имеет только две составляющие поля 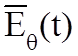 и 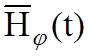, которые в любой точке имеют одинаковую фазу. Амплитуды поля уменьшаются обратно пропорционально расстоянию R и зависят от угла q. Это есть монохроматическая ЭМВ, расходящаяся в радиальных направлениях, скорость распространения:

                             

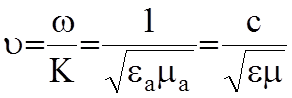
Векторы  и  взаимно-перпендикулярны и образуют с вектором Пойнтинга правую тройку векторов:

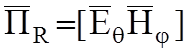                                                                                                        (6.4)

             Вектор Пойнтинга имеет только одну составляющую , это значит, что энергия движется в направлении радиусов только от излучателя. Она не возвращается обратно к излучателю как в ближней зоне, и представляет собой энергию излученной ЭМВ. Скорость переноса энергии совпадает с фазовой скоростью ЭМВ 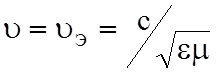. Время t и пространственная координата R, определяющие фазу векторов  и  входят в уравнение (6.3) в виде линейной комбинации 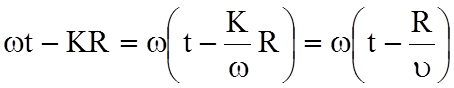, то есть зависимость векторов поля от пространственных координат R и времени t одна и та же. Фаза векторов  и меняется от точки к точке в направлении распространения ЭМВ. Такую ЭМВ называют бегущей ЭМВ (6.3). Волновой поверхностью (фронтом)монохроматической ЭМВ называют геометрическое место точек, в которых в фиксированный момент времени колебания векторов  (и ) имеют одну и ту же фазу, это эквифазная поверхность. Уравнение фронта волны

t-R/u=const в фиксированный момент времени t, переходит в уравнение R=R₁=const. А это есть уравнение сферической волновой поверхности. Таким образом, в дальней зоне поле представляет собой сферические бегущие волны, расходящиеся от излучателя во все стороны вдоль радиусов R со скоростью u и удаляющиеся в бесконечность. Это поле называют полем излучения, а дальнюю зону называют зоной излучения или волновой зоной. Дальнюю зону на практике используют для организации радиосвязи на большие расстояния, так как зависимость векторов поля от расстояния 1/R определяет медленный спад амплитуды поля.

             Рассмотрим зависимость векторов поля от угловых координат q и j. От азимутального угла j векторы поля не зависят. От меридионального угла q зависимость векторов  и одна и та же – это sinq. Зависимость векторов поля от угловых координат q и j называют амплитудной характеристикой направленности, а ее графическое изображение называют диаграммой направленности (ДН).

             Для ЭЭИ характеристика направленности f(q,j)=sinq. Угол q отсчитывается от оси излучателя (рисунок 6.3). Для удобства сравнения различных ДН их строят в нормированном к максимальному значению виде, то есть:

                                           

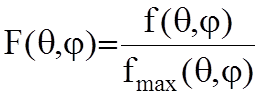
             6.3 Мощность и сопротивление излучения

             Средняя за период мощность излучения, переносимая ЭМПолем определяется через среднее значение :

                               

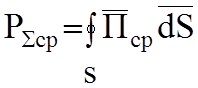
             После интегрирования по замкнутой поверхности сферы с центром в центре излучателя получим:

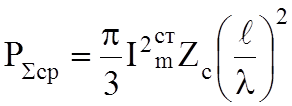                              ,                                                            (6.5)

             где  .

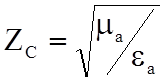Для вакуума ,  и Ом.

             Для сравнения различных излучателей вводят сопротивление излучения , согласно закону Джоуля – Ленца:

                              ; 

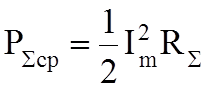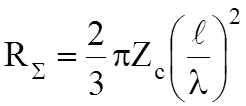
             Для вакуума . Сопротивление излучения должно быть как можно больше, так как при том же токе мощность излучения растет.