Волновые уравнения для векторов поля

             5 ВОЛНОВЫЕ УРАВНЕНИЯ ДЛЯ ВЕКТОРОВ ПОЛЯ

             В большинстве задач электродинамики требуется найти векторы поля по заданным источникам, определение их непосредственно из уравнений Максвелла представляет сложную задачу. Поэтому их преобразуют таким образом, чтобы получить дифференциальные уравнения более удобные для решения задач.

             Для линейной, изотропной и однородной среды в результате преобразований получаются волновые уравнения:

                                   

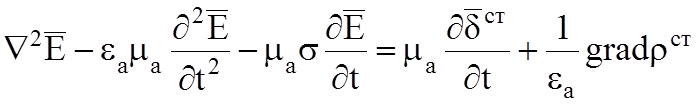
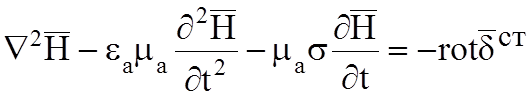                                       ,                  (5.1)                       

             где 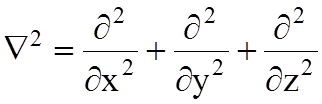- оператор Лапласа, сумма вторых производных от вектора  и  по пространственным координатам.

             В правой части стоят источники ЭМП, они зависят от времени и пространственных координат, поэтому решение (5.1) сложное. Для объема где отсутствуют источники ЭМП и s=0 уравнение упрощается:

                                        

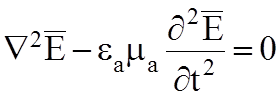
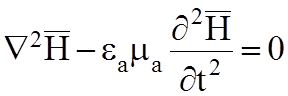                                                                                             (5.2)

             В случае монохроматического ЭМП, переходя к комплексным амплитудам, получим:

                                         

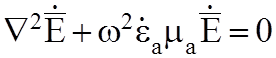
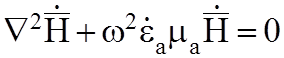                                                                                             (5.3)

             Электродинамические потенциалы. Для определения векторов поля в электродинамике применяют искусственный прием: сначала находят вспомогательные функции, а потом через них вычисляют векторы поля. Такими функциями являются электродинамические потенциалы, вектор Герца и др. Вводятся они так:

, из векторного анализа , отсюда

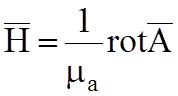                                       ;      ,                                          (5.4)

             где - векторный электродинамический потенциал.

             Подставляя (5.4) во второе уравнение Максвелла получим:

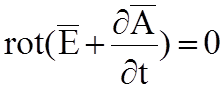                                       , учитывая тождество

                                       , приравниваем .

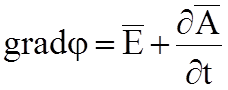             Тогда вектор 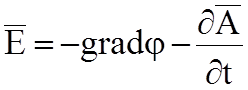.                                                             (5.5)

             Знак минус введен, чтобы в случае электростатического поля функция j совпадала с потенциалом поля. Теперь все векторы поля выражаются через электродинамические потенциалы  и j, следовательно, теперь, надо их рассчитывать. Оказывается, что  и j удовлетворяют таким же волновым уравнениям, но правая часть у них значительно проще и решение соответственно тоже:

                                         

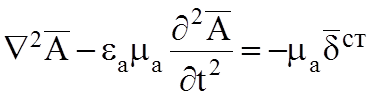
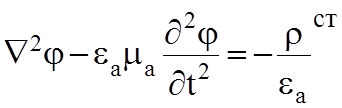                                                                                     (5.6)

             Уравнения вида (5.2)-(5.6) относятся к виду, они описывают:

                                      

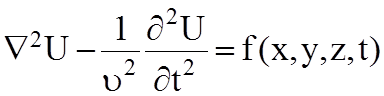
волновые процессы, они хорошо изучены. Параметр u равен скорости этого процесса.

             Поэтому можно сделать вывод о том, что ЭМП существует в виде волнового электромагнитного процесса, описывается волновыми уравнениями вида (5.1, 5.2, 5.3, 5.6). Решением этих уравнений является электромагнитная волна, распространяющаяся со скоростью 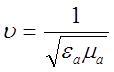, векторы поля зависят от пространственных координат (x, y, z) и времени t.

             Решение волновых уравнений. Общее решение при s=0 уравнений (5.6) имеет вид, для :

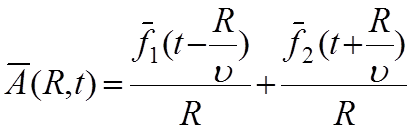                                                                       (5.7)

             где  и - произвольные векторные функции, дважды дифференцируемые. Конкретный их вид зависит от начальных условий. Первая функция от аргумента 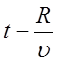 распространяется в сторону увеличения расстояния R от источника в бесконечность, амплитуда зависит от расстояния как , что удовлетворяет условию излучения (4.1). Вторая функция распространяется из бесконечности к источнику, что физически невозможно, и ее можно не рассматривать. С учетом источников ЭМП решение для векторного потенциала   имеет вид:

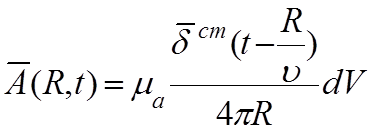                                                                               (5.8)

             Рассмотрим подробнее физический смысл уравнения (5.8).

1.  ЭМП распространяется от своих источников с конечной

скоростью 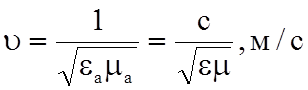 и имеет волновой характер.

2.  В точке наблюдения в момент времени t эл. дин. потенциалы, а

следовательно, и векторы  и , созданные источниками, сосредоточенные в объеме dV, определяются значениями этих источников не в момент времени t, а в некоторый предшествующий момент времени 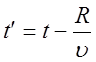 (где R- расстояние от источников до точки наблюдения). Следовательно, воздействие источников достигает точки наблюдения не мгновенно, а через время запаздывания 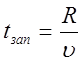, необходимое для распространения ЭМП от источника на расстояние R с конечной скоростью u.

Поэтому решения (5.8) называют запаздывающими решениями, а потенциалы  и j запаздывающими потенциалами. Распространяющееся возмущение от источников в бесконечность называют электромагнитной волной (ЭМВ). Наличие времени запаздывания 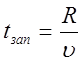 обязательно в ЭМВ.

3.  Геометрическое место точек, до которых дошло эл. м. возмущение,

обусловленное одним и тем же значением источников, называют фронтом ЭМВ. Фронт волны имеет вид сферической поверхности R=const с центром в сосредоточенном источнике. Такую ЭМВ называют сферической. Запаздывающие потенциалы  и j определяют сферическую расходящуюся ЭМВ, которая распространяется от источника во все стороны вдоль радиусов R со скоростью u. Если сосредоточенные источники изменяются по гармоническому закону, то (5.8) принимает вид:

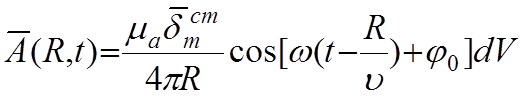                                                           (5.9)

             где j₀ –начальная фаза .

4.  Измеренное вдоль направления распространения монохроматической

ЭМВ расстояние между двумя последовательными точками, в которых колебания

сдвинуты на 2p, называют длиной ЭМВ - l. Из (5.9) имеем:

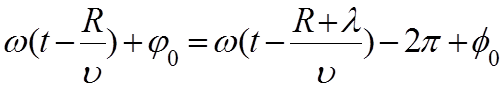                          ,   откуда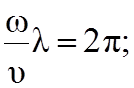     

                                       ; ,

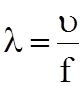             где f – частота ЭМВ, Гц.

             Обозначим 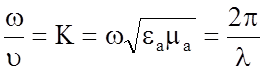, рад/м – параметр K называют волновым числом. Он определяет сдвиг по фазе ЭМВ на длине пути равном длине 1 метр. Произведение 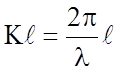- сдвиг по фазе на пути .Наличие этого сдвига на пути (или R) обязательно в распространяющейся ЭМВ.

5.  Пусть теперь сторонние источники поля распределены в конечном объеме V:

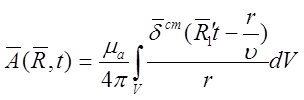                                       ,                                      (5.10)

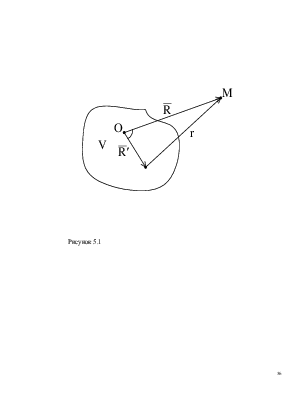
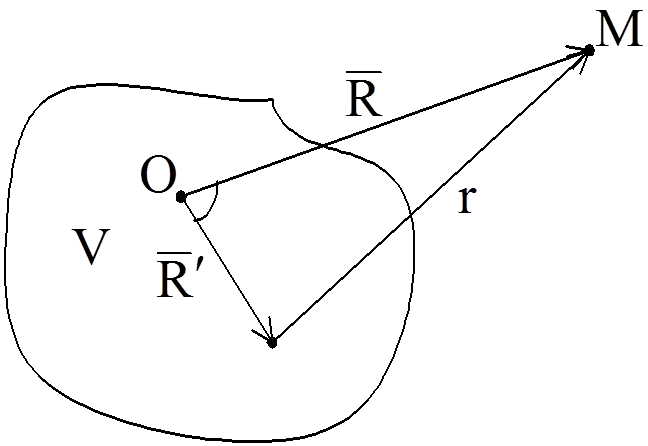
             где - радиус-вектор, характеризующий положения точки наблюдения М относительно начала координат 0;

- радиус – вектор, характеризующий положение сосредоточенного источника :

                                        

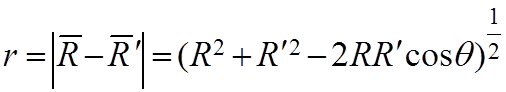
переменное расстояние между точкой наблюдения М и текущей точкой объема V (рисунок 5.1).

             Решение (5.10) для метода комплексных амплитуд:

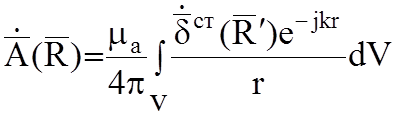                                                                           (5.11)

             Если среда имеет s¹0, то в (5.11)  - заменить на и .

             Рисунок 5.1