








ВВЕДЕНИЕ
Принцип выбора варианта
При изучении курса высшей математики практические занятия по решению задач имеют большое значение для лучшего усвоения теоретического материала. По программе заочной формы обучения по математике студенты третьего курса во втором семестре должны самостоятельно выполнить контрольную работу №12.
Цель настоящих методических указаний − оказать помощь студентам в освоении методики решения типовых задач.
Теоретические сведения, необходимые для решения задач по математической логике и теории графов, приведены в данных методических указаниях, конспекте лекций и работах [1, 2]. Для выбора варианта и номеров задач по варианту необходимо пронумеровать буквы в записи своих фамилии, имени и отчества. Номера букв соответствуют номерам контрольных работ. Например:
|
И |
В |
А |
Н |
О |
В |
О |
Л |
Е |
Г |
П |
Е |
Т |
Р |
О |
В |
И |
Ч |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Из этой записи следует: вариант двенадцатой контрольной работы будет определяться буквой Е. Затем используется таблица, приведенная ниже.
|
Буква |
А, Б, |
В, Г, |
Д, Е, |
Ж, З, И, Й |
К, Л |
М, Н |
О, П |
Р, С, Т |
У, Ф, Х, Ц, Ч |
Ш, Щ, Ы, Ь, Э, Ю, Я |
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Итак, двенадцатой контрольной работе соответствует буква Е, по которой из последней таблицы определяем для этой контрольной работы третий вариант с номерами задач 403, 413, 423.
В пункте 1.1 указаний даны условия задач. В пункте 1.2 по номеру задачи помещен материал, который поможет при ее решении.
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ КОНТРОЛЬНЫХ ЗАДАНИЙ
1.1. Контрольная работа 12
Элементы дискретной математики
З а д а ч и 401 – 410. Даны формулы алгебры логики. Составить по ним таблицы истинности и совершенные дизъюнктивные нормальные формы (СДНФ).
401. ![]() .
.
402. ![]() .
.
403. ![]() .
.
404. ![]() .
.
405. ![]() .
.
406. ![]() .
.
407. ![]() .
.
408. ![]() .
.
409. ![]() .
.
410. ![]() .
.
З а д а ч и 411 – 420. Даны две формулы алгебры логики. Проверить их равносильность двумя способами: а) с помощью таблиц истинности; б) с помощью равносильностей.
411.
![]() .
.
412.
![]() .
.
413.
![]() .
.
414.
![]() .
.
415.
![]() .
.
416.
![]() .
.
417.
![]() .
.
418.
![]() .
.
419.
![]() .
.
420.
![]() .
.
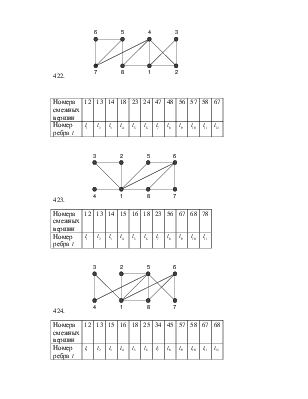
З а д а ч и 421 – 430. Дан граф, вершины которого занумерованы. В таблице приведены номера ребер, соединяющих данные вершины, и длины этих ребер. Найти а) матрицу смежности графа; б) матрицу инцидентности графа; в) все маршруты длины 2, выходящие из вершины 1; г) все простые циклы, проходящие через вершину 1; д) выяснить, будет ли граф связным; е) найти степени всех вершин графа; е) выяснить, будет ли граф эйлеровым; ж) найти остов графа.
421.
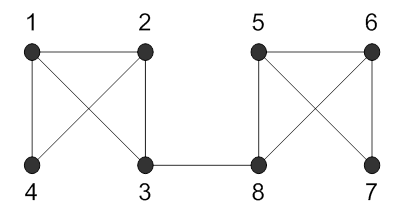
|
Номера смежных вершин |
12 |
13 |
14 |
23 |
24 |
38 |
56 |
57 |
58 |
67 |
68 |
|
Номер ребра |
|
|
|
|
|
|
|
|
|
|
|
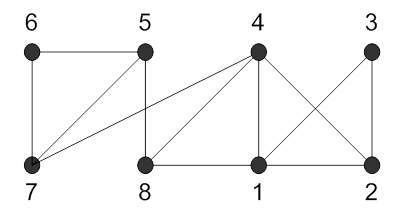
422. 
|
Номера смежных вершин |
12 |
13 |
14 |
18 |
23 |
24 |
47 |
48 |
56 |
57 |
58 |
67 |
|
Номер ребра |
|
|
|
|
|
|
|
|
|
|
|
|
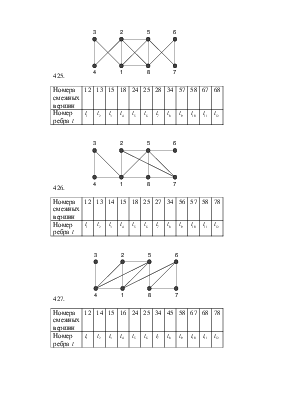
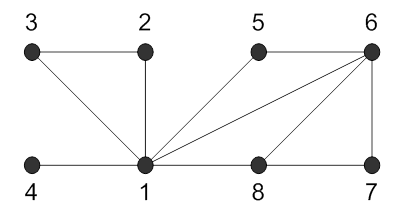
423. 
|
Номера смежных вершин |
12 |
13 |
14 |
15 |
16 |
18 |
23 |
56 |
67 |
68 |
78 |
|
Номер ребра |
|
|
|
|
|
|
|
|
|
|
|
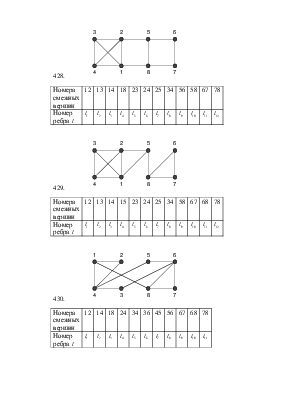
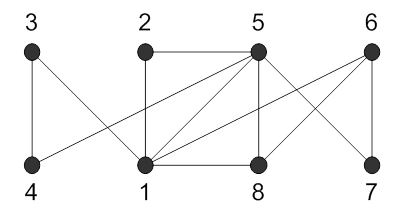
424. 
|
Номера смежных вершин |
12 |
13 |
15 |
16 |
18 |
25 |
34 |
45 |
57 |
58 |
67 |
68 |
|
Номер ребра |
|
|
|
|
|
|
|
|
|
|
|
|
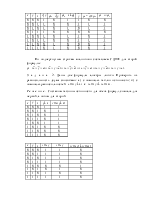
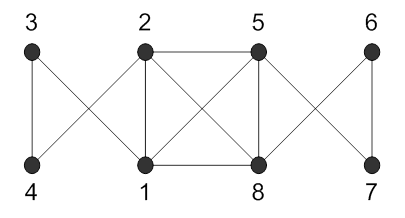
425. 
|
Номера смежных вершин |
12 |
13 |
15 |
18 |
24 |
25 |
28 |
34 |
57 |
58 |
67 |
68 |
|
Номер ребра |
|
|
|
|
|
|
|
|
|
|
|
|
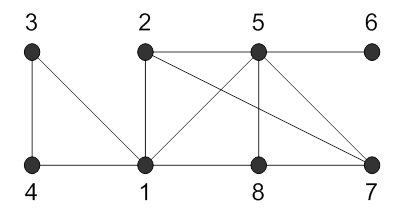
426. 
|
Номера смежных вершин |
12 |
13 |
14 |
15 |
18 |
25 |
27 |
34 |
56 |
57 |
58 |
78 |
|
Номер ребра |
|
|
|
|
|
|
|
|
|
|
|
|
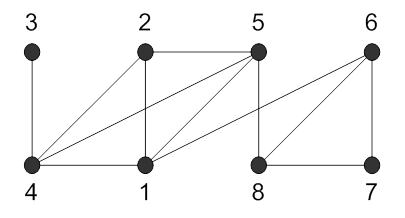
427. 
|
Номера смежных вершин |
12 |
14 |
15 |
16 |
24 |
25 |
34 |
45 |
58 |
67 |
68 |
78 |
|
Номер ребра |
|
|
|
|
|
|
|
|
|
|
|
|
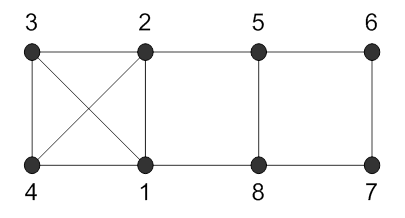
428. 
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.