З
а д а ч а 2. Даны две формулы алгебры логики. Проверить их равносильность
двумя способами: а) с помощью таблиц истинности; б) с помощью равносильностей: ![]() .
.
Р е ш е н и е. Составим таблицы истинности для обеих формул, сначала для первой, а потом для второй.
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
0 |
Поскольку таблицы истинности для обеих формул различны, то формулы не равносильны.
Воспользуемся
теперь равносильностями алгебры логики и найдем для данных формул равносильные,
выраженные через конъюнкцию, дизъюнкцию и отрицание. Для первой формулы: ![]()
Для
второй формулы: ![]()
Полученные две формулы, равносильные исходным, различны, поэтому и исходные две формулы не равносильны.
З а д а ч а 3. Дан граф, вершины которого занумерованы. В таблице приведены номера ребер, соединяющих данные вершины, и длины этих ребер. Найти а) матрицу смежности графа; б) матрицу инцидентности графа; в) все маршруты длины 2, выходящие из вершины 1; г) все простые циклы, проходящие через вершину 1; д) выяснить, будет ли граф связным; е) найти степени всех вершин графа; е) выяснить, будет ли граф эйлеровым.
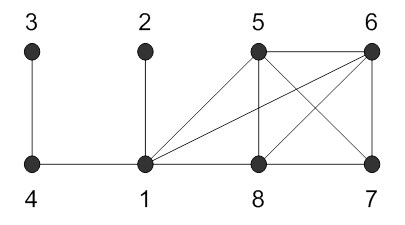
|
Номера смежных вершин |
12 |
14 |
15 |
16 |
18 |
34 |
56 |
57 |
58 |
67 |
68 |
78 |
|
Номер ребра |
|
|
|
|
|
|
|
|
|
|
|
|
Р
е ш е н и е. Найдем матрицу смежности данного графа. Поскольку у графа 8
вершин, то матрица смежности будет квадратной матрицей 8-го порядка. Поскольку
граф является простым и не является ориентированным графом, поэтому матрица
смежности будет симметричной и заполнена только нулями и единицами. Поскольку
первая вершина является смежной с вершинами 2, 4, 5, 6 и 8, то единицам в
матрице смежности будут равны элементы: ![]() ,
, ![]() ,
,![]() ,
,![]() и
и
![]() первой строки. Остальные элементы первой
строки будут равны нулю. Аналогично находятся элементы всех оставшихся строк
матрицы смежности. Запишем окончательный вид матрицы смежности данного графа.
первой строки. Остальные элементы первой
строки будут равны нулю. Аналогично находятся элементы всех оставшихся строк
матрицы смежности. Запишем окончательный вид матрицы смежности данного графа.

Найдем
вид матрицы инцидентности данного графа. Поскольку в графе 8 вершин и 12 ребер,
следовательно, матрица будет иметь размер 8×12. Первая вершина инцидентна
ребрам l1,
l2,
l3,
l4
и l5,
то в первой строке матрицы единице будут равны элементы ![]() ,
,
![]() ,
, ![]() ,
, ![]() и
и ![]() .
Остальные элементы первой строки матрицы инцидентности будут равны нулю.
Аналогично находятся элементы остальных строк матрицы инцидентности. Запишем
окончательный вид матрицы инцидентности данного графа.
.
Остальные элементы первой строки матрицы инцидентности будут равны нулю.
Аналогично находятся элементы остальных строк матрицы инцидентности. Запишем
окончательный вид матрицы инцидентности данного графа.
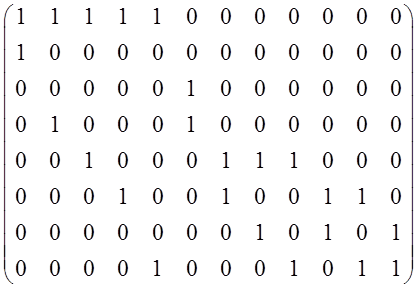
Заметим, что в каждом столбце матрицы инцидентности простого графа без петель должно присутствовать только две единицы, а остальное – нули.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.