Элементы дискретной математики: Методические указания к выполнению контрольной работы, страница 2

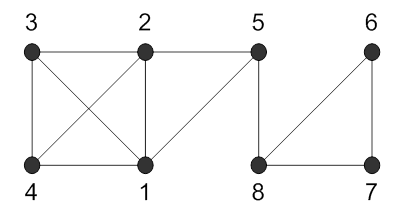
Номера смежных вершин	12	13	14	18	23	24	25	34	56	58	67	78
Номер ребра

429.            

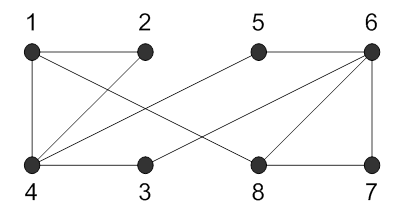
Номера смежных вершин	12	13	14	15	23	24	25	34	58	67	68	78
Номер ребра

430.            

Номера смежных вершин	12	14	18	24	34	36	45	56	67	68	78
Номер ребра

1.2. Примеры решения задач

З а д а ч а  1. Даны формулы алгебры логики. Составить по ним таблицы истинности и совершенные дизъюнктивные нормальные формы (СДНФ).

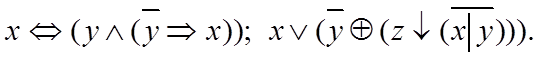
Р е ш е н и е.  Составим таблицу истинности для первой формулы . Будем строить ее последовательно в соответствии с шагами построения формулы . При построении используем определения логических операций, входящих в состав формулы .

0	0	1	0	0	1
0	1	0	1	1	0
1	0	1	1	0	0
1	1	0	1	1	1

Таблица истинности для первой формулы построена.

Составим СДНФ, равносильную исходной формуле. Выделим строки таблицы истинности формулы , в которых . Элементы данных строк подчеркнуты снизу. По этим строкам будем составлять СДНФ. Количество конъюнкций в СДНФ равно количеству строк таблицы истинности формулы , в которых . В нашем случае таких конъюнкций будет две. По каждой из строк составляем конъюнкции следующим образом: если соответствующее значение аргумента в строке таблицы истинности равно 0, то соответствующий аргумент входит в конъюнкцию с отрицанием, если 1, то без отрицания. Таким образом, по первой строчке таблицы истинности получаем конъюнкцию , по четвертой - . Собирая их через дизъюнкцию, получаем СДНФ, равносильную исходной формуле:

. СДНФ для первой формулы построена.

Аналогично с использованием определений штриха Шеффера, стрелки Пирса и кольцевой суммы составим таблицу истинности для второй формулы .

0	0	0	1	0	1	1	0	0
0	0	1	1	0	0	1	1	1
0	1	0	1	0	1	0	1	1
0	1	1	1	0	0	0	0	0
1	0	0	1	0	1	1	0	1
1	0	1	1	0	0	1	1	1
1	1	0	0	1	0	0	0	1
1	1	1	0	1	0	0	0	1

          По подчеркнутым строкам аналогично составляем СДНФ для второй формулы: .