11 Построение кривых движения
Расчет и построение кривых движения могут быть выполнены аналитическим или графическим методом. При аналитическом методе расчета [1, 2] для любого интервала скоростей принимается постоянной ускоряющая сила. Движение поезда при этом будет равноускоренным.
При принятом условии
![]() (11.1)
(11.1)
где υ1 – скорость в начальное время t = 0, км/ч;
υ2 – скорость в конце отрезка времени ∆ t, км/ч;
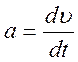 – ускорение движения, км/ч2;
– ускорение движения, км/ч2;
∆ t – отрезок времени, в течение которого определяется изменение скорости.
Из формулы (11.1) следует:
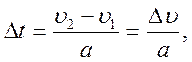 (11.2)
(11.2)
где ∆υ = υ2 - υ1 — приращение скорости за время ∆ t, км/ч.
Если в формулу (11.2) подставить значение а из уравнения (9.9), то получим
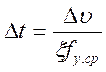 ,
(11.3)
,
(11.3)
где fу.ср – среднее значение удельной ускоряющей силы при изменении скорости от υ1 до υ2, Н/кН.
Равенство (11.3) позволяет определить время, в течение которого скорость поезда при действии заданной удельной ускоряющей (замедляющей) силы изменяется в пределах от υ1 до υ2.
Средняя скорость движения поезда в интервале времени
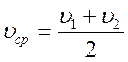 .
(11.4)
.
(11.4)
Тогда путь, пройденный поездом,
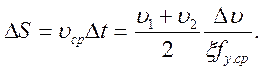 (11.5)
(11.5)
Так как ∆υ = υ1- υ2, то формула (11.4) может быть записана в следующем виде:
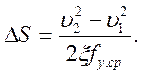 (11.6)
(11.6)
Формулы (11.3) и (11.6) позволяют определить время и путь, проходимый поездом в каждом интервале скоростей. Для определения пройденного поездом пути, а также полного времени хода поезда расчеты повторяются, а затем суммируются. По вычисленным значениям ∆t и ∆S могут быть также построены и кривые движения. Аналитический метод решения уравнения движения поезда требует большого числа вычислений и значительных затрат времени, поэтому применение его возможно при использовании ЭВМ [1, 2].
Графические методы построения кривых движения отличаются от аналитического тем, что ∆t и ∆S не вычисляются, а находятся геометрическими построениями. Эти методы имеют много разновидностей. Наибольшее распространение получил метод А. И. Липеца – Г. В. Лебедева, рекомендованный Министерством путей сообщения для практического использования и получивший название «способа МПС». Ниже рассмотрены основные положения этого метода.
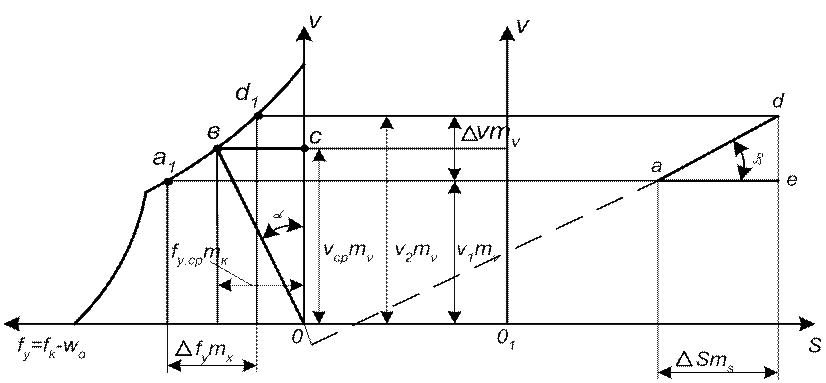
Рисунок 11.1 – Построение кривой скорости в функции пути графическим способом
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.