11.1 Построение кривой скорости движения поезда υ(S).
Пусть нам задана (рисунок 11.1) кривая ускоряющих сил в произвольном масштабе mк, мм/Н/кН, соответствующая определенной серии электровоза и массе поезда, а на кривой скорости υ(S) задан участок аd, на котором произошло изменение скорости ∆υmv=(υ2—υ1)mv на участке пути ∆Sms(mv и ms – соответственно масштабы скорости и пути).
Приращению скорости ∆υmv соответствует участок на кривой ускоряющих сил. Средней скорости на участке аd будет соответствовать и среднее значение ускоряющей силы fу.ср (точка b). Обозначим угол между прямой оb и осью ординат через α, а угол между прямой аd и осью абсцисс – через β.
Из рассмотренных кривых fу(υ) и υ(S) следует:
1) угол β определяет приращение скорости ∆υmv на участке пути ∆Sms, с увеличением угла β приращение скорости возрастает, а следовательно, увеличивается и средняя скорость υсрmv на участке пути ∆Sms;
2) приращение скорости зависит от ускоряющей силы fуmк, среднее значение которой на данном участке а1d1 характеризуется углом α, чем больше угол α, тем больше fу.ср, а следовательно, больше приращение скорости;
3) характер изменения скорости движения поезда одинаково влияет на изменение углов α и β.
Определим возможность нахождения угла β графическим путем. Из треугольника аdе следует, что
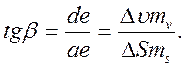 (11.7)
(11.7)
Так как ∆S = υср∆t, то
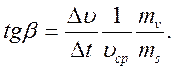 (11.8)
(11.8)
Из треугольника оbс следует, что
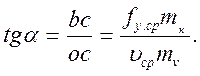 (11.9)
(11.9)
В соответствии с уравнением движения поезда (64) удельная ускоряющая (замедляющая) сила
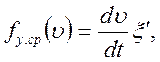 (11.10)
(11.10)
где
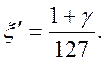
Следовательно,
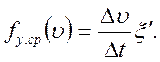 (11.11)
(11.11)
Тогда
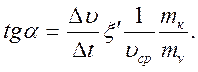 (11.12)
(11.12)
Рассмотрим условие, при котором угол α будет равным углу β. Для этого приравняем правые части равенств (11.8) и (11.12):
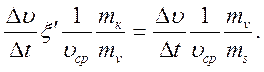 (11.13)
(11.13)
Из уравнения (11.13) следует, что
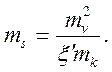 (11.14)
(11.14)
Выбрав масштабы в соответствии с равенством (11.14) (обычно принимают удобные масштабы mv и mх, а масштаб ms вычисляют), мы обеспечиваем равенствo углов α и β, а следовательно, прямая аd при этом будет перпендикулярна прямой оb и ее можно провести, пользуясь линейкой и угольником.
При выполнении тяговых расчетов рекомендуются практически удобные масштабы для грузовых и пассажирских поездов, которые приведены в таблице 11.1
Таблица 11.1 – Масштабы, рекомендуемые при построении кривых движения
|
Масштаб |
Значение масштабов для грузовых и пассажирских поездов при 1+γ = 1,06 |
|
|
mv, мм/км/ч mк, мм/Н/кН ms, мм/км mt, мм/с ∆, мм |
1 |
2 |
|
6 20 1/6 30 |
12 40 1/6 30 |
|
Кривая скорости υ(S) строится по кривым ускоряющих и замедляющих сил с момента трогания поезда в следующей последовательности.
1. Задаются первым приращением скорости ∆υ1, (при следовании электровоза под током до выхода на автоматическую характеристику – не более 10 км/ч; после выхода на автоматическую характеристику – не более 5 км/ч; при следовании на выбеге – не более 10 км/ч; в режиме торможения при скорости свыше 50 км/ч – не более 10 км/ч; при скорости от 50 км/ч до нуля – не более 5 км/ч) и на кривой ускоряющих усилий отмечают точку А (рисунок 11.2), соответствующую средней скорости, с которой поезд будет следовать на первом отрезке пути. На точки А и О1 накладывается линейка, а затем с помощью прямоугольного треугольника проводится прямая О2А1 под углом 90° к прямой О1А до пересечения с горизонталью, соответствующей приращению скорости.

Рисунок 11.2 – Построение кривой скорости в режиме тяги на горизонтальном участке пути
Затем задаются вторым приращением скорости ∆υ2 и аналогично строят прямую А1В1 и т. д.
2) При разгоне и движении поезда, например, по подъему I = +3‰ удельная ускоряющая сила fу=fк-wо-w1. Следовательно, fу уменьшается на величину сопротивления от уклона и кривая fу (υ) сместится вправо на величину wi (кривая 2, рисунок 11.3).
Если разгон и движение поезда происходит на спуске, то fу=fк-wо-w1 и, следовательно, кривая fу(υ) смещается влево (кривая 3 на рисунке 11.3).
Для того чтобы каждый раз не перестраивать кривую ускоряющих усилий, начало системы координат (точку О1) переносят влево (при подъеме) или вправо (при спуске) на величину, равную w1=±i.
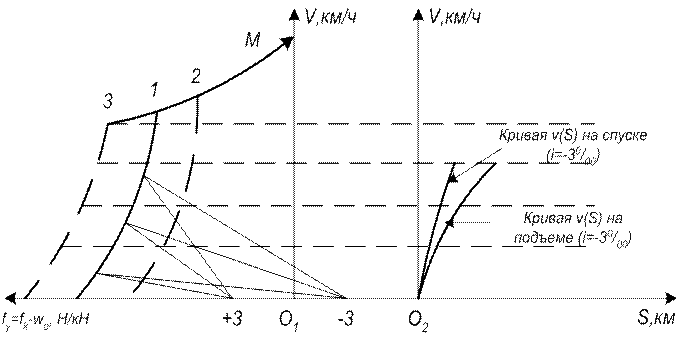
Рисунок 11.3 – Построение кривой скорости в режиме тяги на уклоне
3) Если удельная ускоряющая сила будет равна сопротивлению движения от подъема (fк-w0 = wi), то движение поезда будет равномерным и кривая скорости υ(S) будет располагаться параллельно оси абсцисс.
4) При движении поезда по площадке установившаяся скорость характеризуется точкой пересечения кривой (fк-w0) с осью ординат (точка М, рисунок 11.3).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.