ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ И РИСКА И КОНФЛИКТНЫХ СИТУАЦИЯХ
Конфликтными называются ситуации, в которых интересы привлеченных сторон являются полностью или частично противоположными.
Каждая конфликтная ситуация является достаточно сложной. Для проведения ее экономико-математического анализа необходимо абстрагироваться от некоторых факторов и построить модель ситуации. При этом должны быть известны возможные варианты поведения участников – правила игры, и результаты, к которым приводят различные комбинации действий участников конфликта.
В 1940х годах Дж.фон Нейман и О.фон Моргенштерн как игру с помощью математический методов описали характерные для рыночной среды явления конкуренции.
ИГРА – это формализованное описание или модель конфликтной ситуации, которая содержит четко выраженные правила действий ее участников, которые пытаются получить некоторое преимущество с помощью выбора конкретной стратегии поведения.
Неопределенность результатов игры происходит вследствие ряда причин. Виды игровых моделей:
· Особенности правил игры приводят к такому количеству вариантов ее развития, что предвидеть результаты игры практически невозможно. Такие игры называют комбинаторными;
· Источником неопределенности является влияние случайных факторов. Игры, в которых результат неопределен только из-за случайных причин, называются азартными;
· Неопределенность обуславливается отсутствием информации про действия и стратегию противника. Такие игры называются стратегическими.
Лицо принимающее решение называется игроком.
Стратегия игрока – это план, в соответствии с которым игрок осуществляет выбор своих действий в какой-либо возможной ситуации при какой-либо возможной информации.
Теория игр. Матричные игры могут служить математическими моделями многих конфликтных ситуаций из области экономики. При этом конфликт не обязательно является антагонистическим, в качестве конфликта можно рассматривать любое разногласие.
Всякая теоретико-игровая модель должна отражать, кто, как и в какой форме конфликтует, а также, интерес игроков в том, или ином исходе конфликта.
Содержание математической теории игр состоит:
1) в установлении принципов оптимального поведения игроков в играх;
2) в доказательстве существования ситуаций, которые складываются в результате применения этих принципов;
3) в разработке методов фактического нахождения таких ситуаций.
Содержание теории игр состоит в установлении связей между компонентами каждой игры и оптимальными ее исходами, и, прежде всего, в уточнении самого понятия оптимальности, в доказательстве существования оптимальных исходов и в их фактическом определении. Риск и неопределенность исходов игры обуславливаются случайным соотношением среды или вероятностным характером появления желаемого результата по возможным стратегиям.
Нам необходимо рассмотреть ситуации, в которых риск связан с совокупностью неопределенных факторов среды. В играх с неопределенной средой, как и в стратегических играх, создание модели начинается с построения исходной матрицы.
Независимо от вида матрицы игры, требуется выбрать такую стратегию игрока, которая была бы наиболее выгодной по сравнению с другими.
Неопределенность, связанную с отсутствием информации о вероятностях состояния среды, называют «безнадежной». В таких случаях, для определения наилучших решений используются критерии: Лапласа, Сэвиджа, Гурвица, Вальда.
При выборе оптимального решения нецелесообразно останавливаться на выборе одного из критериев, так как в ряде случаев это может привести к неоправданным результатам при выборе решения, ведущим к значительным потерям любого содержания. Поэтому имеет смысл применять несколько критериев в совокупности.
Применение различных критериев для различных задач выбора оптимального решения в условиях неопределенности показывает, что подход, базирующийся на комплексном применении указанных критериев, может стать определяющим.
Данные, необходимые для принятия решения, задаются в виде матрицы, строки которой соответствуют возможным методам управления риском, а столбцы – возможным состояниям среды. Таких состояний два: в случае проявления негативной стороны риска или в случае отсутствия потерь от риска.
Каждому методу и возможному состоянию среды соответствует результат, определяющий потери предприятия при выборе данного метода управления и реализации данного состояния среды.
Критерий Лапласапредполагает, что если нет достаточных оснований считать, что вероятность того или иного решения имеют неравномерное распределение, то они принимаются одинаковыми. Тогда задача сводится к поиску наиболее оптимального варианта. Этот оптимальный вариант может сводиться к поиску как максимального значения (если речь идет о прибыли), так и минимального (если речь идет о потерях).
Исходную задачу можно рассматривать как задачу принятия решения в условиях неопределенности, когда выбирается действие, дающее наименьшие потери.
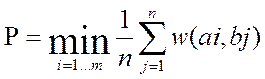 , (3.1)
, (3.1)
где P –оптимальное решение;
1/n – вероятность реализации состояния;
W (ai,bj) – оптимальная стратегия при данных значениях;
ai – действие при минимальных потерях;
bj - действие при максимальных потерях.
Пример 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.