Принятия решений в условиях неопределенности и риска и конфликтных ситуациях, страница 2

Предприятию необходимо сделать выбор в пользу одной из стратегий управления производственным риском, чтобы застраховаться от возможных потерь в течение следующего года.

Ре­зультат развития производственной ситуации полностью неопределен, но ожидается, что наиболее эффективными стратегиями в сложившихся ус­ловиях будут стратегии управления рисками w1,w2,w3.

Для каждого из двух возможных вариантов развития ситуации существует наилучшая из трех рассматриваемых предприятием стратегий (с точки зрения минимизации возможных потерь).

В таблице  приве­дены возможные потери предприятия.

Таблица 3.1 

Матрица потерь

Стратегии	Потери
	в случае максимальных потерь от риска (bi)	в случае минимальных потерь от риска (ai)
W1	70	8
W2	35	10
W3	40	25

Принцип Лапласа предполагает, что a_i и b_i равновероятны. Следо­вательно, n =2, и ожидаемые потери при выборе методов w₁ ,w₂ ,w₃ составят:

П(w₁) = (1/2)х(70+8) = 39;

П(w₂)= (1/2)х(35+10) =22,5;

П(w₃)=(1/2)(40+25)=32,5.

Таким образом, наилучшим методом управления производствен­ным риском в соответствии с критерием Лапласа будет метод w_{2 .}

Критерий Вальда (минимакс) является наиболее осторожным, по­скольку он основывается на выборе наилучшей из наихудших возможно­стей. То есть, для каждого решения выбирается худшая ситуация (максимальные потери) и среди них отыскивается та, которая принесет максимальный эффект (лучшая из худших).

M = MIN MAX w(b_i, a_i)

Пример 2.

Рассмотрим задачу 1. Необходимые результаты вычисления приведены в таблице, из которой видно, что лучшим ме­тодом управления производственным риском по минимаксу будет w3.

Таблицы 3.2

Матрица потерь

Стратегия	bi	ai	MAX (w(bi,ai)}
w1	70	8	70
w2	35	10	35
w3	40	25	40(минимакс)

Критерий Сэвиджа. Суть этого критерия – в достижении минимального риска. При выборе стратегии по этому методу необходимо составить матрицу потерь (сожалений). Элементы этой матрицы отражают убытки от ошибочного действия или выгоду, упущенную в результате принятия определенного решения в соответствующем состоянии. Расчет элементов новой матрицы производится по формуле:

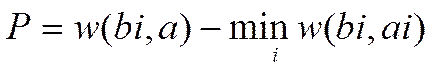                                                                 (3.2)

Пример 3

Рассмотрим исходную задачу

По столбцу b_i  минимальное значение 35:

70 – 35 = 35

35 – 35 = 0

40 – 35 = 5

По столбцу a_i  минимальное значение 8:

8 – 8 = 0

10 – 8 = 2

25 – 8 =17

Таким образом, наша новая матрица выглядит следующим образом:

Таблица 3.3

Матрица

Стратегии	bi	ai	Max(bi,ai)
w1	35	0	35
w2	0	2	2
w3	5	17	17

Последний столбец матрицы мы получаем с помощью выбора максимального значения между значениями b_i и a_i  соответственно.

Согласно данному критерию из полученных значений потерь мы выбираем минимальное. Следовательно, наилучшей будет стратегия w₂.

Критерий Гурвица устанавливает баланс между случаями
крайнего оптимизма и крайнего пессимизма взвешиванием обоих спосо­бов
поведения с соответствующими весами α и  1- α, где 0 ≤ α ≤ 1. Если
выбранная стратегия представляет потери или затраты, критерий выбирает действие, при котором полученный результат рассчитывается по формуле:

                                  (3.3)

Параметр α определяется как показатель оптимизма:

-  при α = 1 кри­терий слишком оптимистичный;

-  при α = 0 он слишком пессимистичный.

-  значение α между 0 и 1 может определяться в зависимости от склонно­сти лица, принимающего решение, к пессимизму или оптимизму. При отсутствии ярко выраженной склонности α = 1/2 представляется наиболее разумным.

Пример 4.

Рассмотрим задачу 1. Положим   α = 1/2. тогда:

(70 + 8)*1/2 = 39

(35 + 10)*1/2 =22.5

(40 + 25)*1/2 = 32.5

Таблица 3.4

Матрица

Стратегии	bi	ai	R
w1	70	8	39
w2	35	10	22.5
w3	40	25	32.5

Оптимальной будет стратегия, имеющая минимальные потери, а именно- w_{2 .}

Для выбора метода управления производственным риском рекомендуется воспользоваться способом, представленным в таблице. А именно: оптимальное решение должно определяться большинством из перечисленных критериев.

Таблица 3.5

Выбор оптимальной стратегии управления риском

Критерий	Потери по стратегиям			Оптимальная стратегия
	W1	W2	W3
Лапласа	39	22,5	32,5	W2
Вальда (минимакс)	70	40	35	W3
Сэвиджа	35	2	17	W2
Гурвица	39	22,5	32,5	W2
Оптимальная стратегия по большинству критериев				W2

Используя данный  подход по разработке модели управления рисками на предприятии, а также вариант конечного выбора критериев выбора оптимального решения по минимизации рисков на предприятии позволяет в значительной степени упростить процесс управления риском.