Теория полезности. Этапы построения функции полезности

7. Теория полезности

Полезность – степень удовлетворения субъекта от потребления товара (получения услуги) или исполнения какого-либо действия.

При решении задач, связанных с выбором оптимального решения в условиях риска и неопределенности, используют теорию игр или теорию полезности.

Принцип оптимальности принятия решений для этих задач можно описать с помощью функции полезности.

Полезность рассматривают как обобщенный показатель выигрыша или проигрыша, когда все ценности сведены в одну шкалу.

Для определения полезности в условиях риска используют общепринятое понятие лотереи, где эксперту предлагают для сравнения 2 альтернативы:

·  Значение показателя Х

·  Лотерею: получить Х_min с вероятностью (1-р) или

                                                        Х_max с вероятностью р.

Величину вероятности р изменяют до тех пор, пока значение показателя Х и лотерея L(Хmin , р, Хmax) не станут эквивалентными. Т.Е :

Х  ≈ L(Хmin , р, Хmax)

Полезность наихудшего результата оценивается как:  U(Х_min)=0

Полезность наилучшего результата оценивается как U(Х_max)=1 или 100.

И всегда U(Х_min) < U(Х_max).

ПРИМЕР:

Рассмотреть 2 варианта инвестирования денег и дать рекомендации по инвестированию, если:

·  Сумма инвестирования составляет 20тыс.грн.

·  Вложение в приобретение государственных безрисковых облигаций с доходом 1000грн. Вероятность 100%

·  Участие в лотерее: выигрыш 2100 с вероятностью 50% и накладные расходы, связанные с участием в лотерее 50грн.

Решение:

Средний выигрыш:

·  Приобретение гос.облигаций: 1000х1 = 1000грн.

·  Лотерея: 2100х0.5 – 50х0.5 = 1025грн.

Вывод: относительно среднего выигрыша рассмотренные альтернативы практически эквивалентны и если игрок нейтрален к риску, он выберет второй вариант.

Рациональное поведение (склонность или несклонность к риску) исследовали американские экономисты Джон фон Нейман (1903-1957) и Оскар фон Моргенштерн (1902-1977). Они вывели ее основные аксиомы.

1.  Аксиома 1 (полноты). Если предприниматель сталкивается с 2 цепочками действий, он всегда может определиться с тем, какая из них ему больше подходит, т.е.:

·  X>Y (X более подходит, чем Y)

·  X≥Y (X более подходит или все равно, чем Y)

·  X≈Y (X иY равноценны)

2.  Аксиома 2 (транзитивности). Преимущество различных цепочек действий последовательна, то есть: если X>Y и Y>Z , то X >Z. Это позволяет избежать фактора изменчивости вкусов субъекта (правильный выбор возможен только при условии установленного вкуса)

3.  Аксиома 3 (непрерывности). С условием выполнения аксиомы транзитивности, если субъект с вероятностью 1 может получить альтернативу X с вероятностью р и (1-р) , то относительно альтернатив Y и Z, существует такое р, при котором Х= Y+Z

4.  Аксиома 4 (независимости). Пусть существуют блага Х и  Y, которые по оценке субъекта одинаковы и две лотереи, которые отличаются тем, что одна содержит Х, а другая – Y, тогда две эти лотереи для субъекта тоже одинаковы.

5.  Аксиома 5 (неравных возможностей). Если субъекту предложить две лотереи, которые дают одинаковый выигрыш но с разной вероятностью, то он выберет ту, вероятность которой больше.

6.  Аксиома 6 (сложенной лотереи). Когда выигрышем одной лотереи является билет другой лотереи, то субъект принимает решение из соображений конечного выигрыша.

Полезность варианта Х определяется вероятностью р(Х), при которой лицу, принимающему решения неважно, что выбрать Х-гарантировано или лотерею L(Хmin , р, Хmax)

Этапы построения функции полезности:

1.  определение наилучших и наихудших из возможных допустимых значений показателей и присвоения им значения полезности соответственно от 0 до 100 (измерение полезности удобно производить по 100-бальной шкале)

2.  оценка экспертами промежуточных значений полезности

3.  расчет средних оценок полезности промежуточных показателей, предложенных экспертами (согласование мнений экспертов)

4.  построение функции полезности с помощью метода наименьших квадратов, которая будет показывать отношение субъекта к риску

Средний выигрыш (математическое ожидание) рассчитывается по формуле:

=

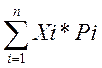
Ожидаемая (средняя) полезность рассчитывается по формуле:

(Х) =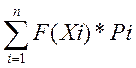, где:

Хi – i-й вариант действия

Рi – вероятность i-го варианта выигрыша

F(Xi) – полезность i-го варианта выигрыша

Необходимо помнить следующие условия взаимосвязи риска и полезности: гарантированная сумма Х, получение которой эквивалентно лотерее, обеспечивает объекту такую полезность, как участие в рискованном деле, то есть F() = (X)

1.  F()> (X), лицо, принимающее решение является склонным к риску. Для него основным является получение гарантированного выигрыша

2.  F()<(X), лицо, принимающее решение является не склонным к риску. Для него основным есть участие в лотерее, рискуя увеличить или потерять гарантированный выигрыш

3.  F()=(X), лицо, принимающее решение является безразлично к риску. Здесь соблюдается условие одинаковой полезности гарантированного выигрыша и участия в лотерее.

Графически это изображается след. образом:

Для варианта склонности к риску, функция полезности растет: чем больше средств имеет субъект, тем больше он хочет получить.

Для варианта нейтрального отношения к риску, функция полезности постоянна

Для варианта несклонности к риску, функция полезности уменьшается,

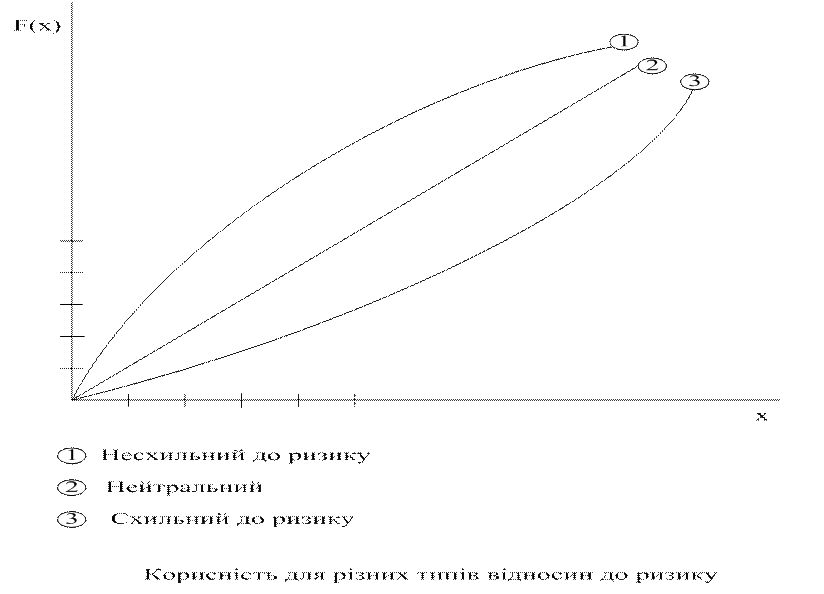
Т.О. отношение к риску зависит не только от особенностей характера и психологии субъекта, но и от его финансового состояния, то есть от  того, какую часть составляет «рисковая» часть суммы от общего финансового состояния субъекта. Чем меньше эта сумма от общего бюджета, тем более вероятно проявление склонности к риску.