



Новосибирский Государственный Архитектурно-Строительный Университет
Кафедра прикладной математики
Отчет по лабораторной работе №1
Часть 2: Решение нелинейных алгебраических уравнений
Выполнил студент 321 гр
Ахмеров К. Р.
Проверил: Федорченко И.А.
Новосибирск
2010
1. Постановка задачи.
Найти решение системы не линейных уравнений Ax̅=b̅, где
|
A = |
4 |
-2 |
-1 |
0 |
b = |
1 |
|
-2 |
4 |
0 |
1 |
2 |
||
|
-1 |
0 |
4 |
2 |
3 |
||
|
0 |
1 |
2 |
4 |
4 |
2. Методы решения.
2.1. Метод обратной матрицы x̅ = A-1 b̅, используя функции Excel МУМНОЖ и МОБР.
Результаты вычислений:
|
Обратная матрица |
||||
|
A-1 = |
0,419048 |
0,247619 |
0,180952 |
-0,15238 |
|
0,247619 |
0,419048 |
0,152381 |
-0,18095 |
|
|
0,180952 |
0,152381 |
0,419048 |
-0,24762 |
|
|
-0,15238 |
-0,18095 |
-0,24762 |
0,419048 |
|
|
х = |
0,847619 |
|
0,8190476 |
|
|
0,752381 |
|
|
0,4190476 |
2.2. Метод простой итерации с точностью ε=0.001. Метод простой итерации заключается в:
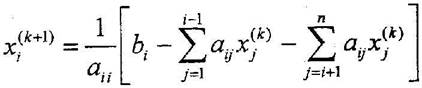
Где k – номер итерации, n – количество уравнений, xi(0) – начальное приближение.
Расчет выполняется с помощью языка Pascal. Листинг программы:
1 uses crt;
2 const A:array[1..4,1..4] of real=( (4,-2,-1,0),(-2,4,0,1), (-1,0,4,2), (0,1,2,4));
3 b:array[1..4] of integer=(1,2,3,4);
4 var matr:array[0..100,0..5] of real;
5 i,j:integer;
6 begin
7 clrscr;
8 for i:=0 to 5 do matr[0,i]:=0;
9 i:=0;
10 writeln(' k x1 x2 x3 x4 pogr');
11 repeat
12 i:=i+1;
13 matr[i,0]:=i;
14 matr[i,1]:=(1+2*matr[i-1,2]+matr[i-1,3])/4;
15 matr[i,2]:=(2+2*matr[i-1,1]-matr[i-4,4])/4;
16 matr[i,3]:=(3+matr[i-1,1]-2*matr[i-1,4])/4;
17 matr[i,4]:=(4-matr[i-1,2]-2*matr[i-1,3])/4;
18 matr[i,5]:=0;
19 for j:=1 to 4 do
20 if abs(matr[i,j]-matr[i-1,j])>matr[i,5] then
21 matr[i,5]:=abs(matr[i,j]-matr[i-1,j]);
22 write(i,' ');
23 for j:=1 to 5 do write(matr[i,j]:8:4);
24 writeln;
25 until matr[i,5]<0.001;
26 readln;
27 end.
Результат вычислений:
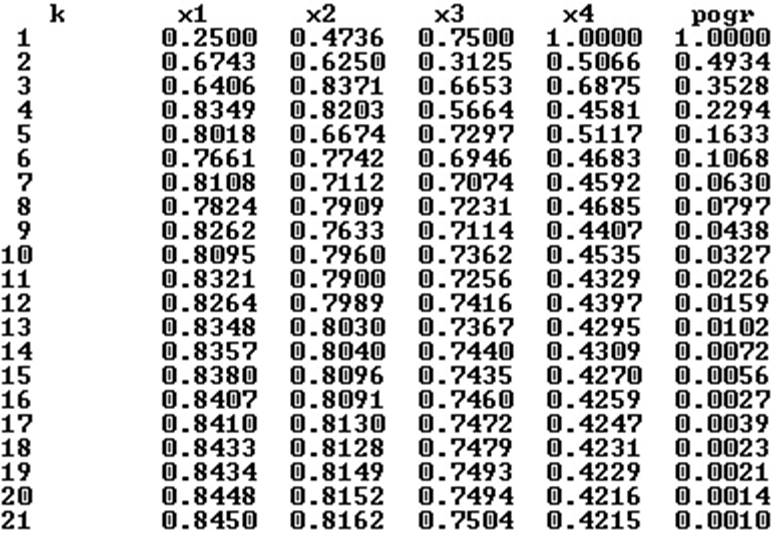
2.3. Метод Гаусса-Зейделя с точностью ε=0.001. Метод заключается в:
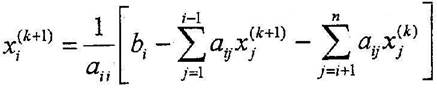
Где k – номер итерации, n – количество уравнений, xi(0) – начальное приближение.
Расчет выполняется с помощью языка Pascal. Листинг программы:
1 const A:array[1..4,1..4] of real=((4,-2,-1,0),(-2,4,0,1),
(-1,0,4,2),(0,1,2,4));
2 b:array[1..4] of integer=(1,2,3,4);
3 var matr:array[0..100,0..5] of real;
4 i,j:integer;
5 begin
6 for i:=0 to 5 do matr[0,i]:=0;
7 i:=0;
8 writeln(' k x1 x2 x3 x4 pogr');
9 repeat
10 i:=i+1;
11 matr[i,0]:=i;
12 matr[i,1]:=(1+2*matr[i-1,2]+matr[i-1,3])/4;
13 matr[i,2]:=(2+2*matr[i,1]-matr[i-1,4])/4;
14 matr[i,3]:=(3+matr[i,1]-2*matr[i-1,4])/4;
15 matr[i,4]:=(4-matr[i,2]-2*matr[i,3])/4;
16 matr[i,5]:=0;
17 for j:=1 to 4 do
18 if abs(matr[i,j]-matr[i-1,j])>matr[i,5] then
19 matr[i,5]:=abs(matr[i,j]-matr[i-1,j]);
20 write(i,' ');
21 for j:=1 to 5 do write(matr[i,j]:8:4);
22 writeln;
23 until matr[i,5]<=0.001;
24 readln;
25 end.
Результат вычислений:

3. Вывод: Результаты, т.е. корни СЛАУ, полученные разными методами, примерно одинаковые. Самым точным является метод обратной матрицы. Из приближенных методов, скорость сходимости метода Гаусса-Зейделя много выше, чем метода простой итерации.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.