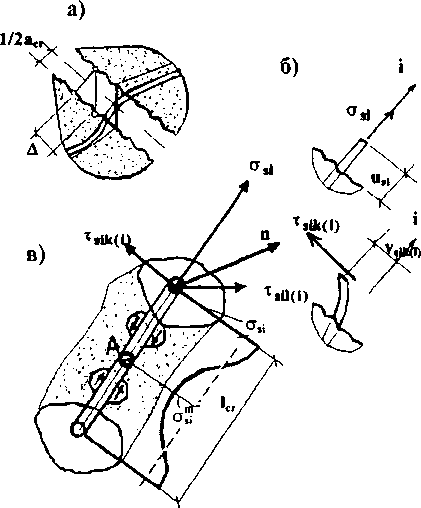
Физические зависимости сначала устанавливаются в локальных координатах n, m, I, нормальных к трещинам, а затем переводятся в глобальную систему х. у, z. Как и прежде, каждое направление армирования задается коэффициентом армирования μsiи таблицей направляющих косинусов относительно локальной системы n, m, I (рис. 7.5,а). Количество арматуры, пересекающей грани единичного куба, показано на рис. 7.5,7.6. Напряжения по граням такого элемента (рис. 7.6) формируются по-разному. На площадках-трещинах действуют нормальные и касательные напряжения в арматуре в зоне трещины, а на других площадках учитываются только средние напряжения σst. Общие напряжения (рис. 7.7,а) получаются суммированием напряжений в бетоне (рис. 7.7,7.6) и в арматуре (рис. 7.7,в).
Проецируя усилия, приложенные к граням элемента (см. рис. 7.6), на оси n, m, I, получим составляющие общих напряжений. Например, нормальные относительных деформаций бетона между трещинами (εbr,l* bkr,l* brk).
 |
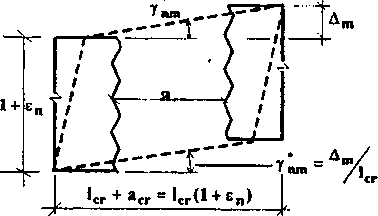
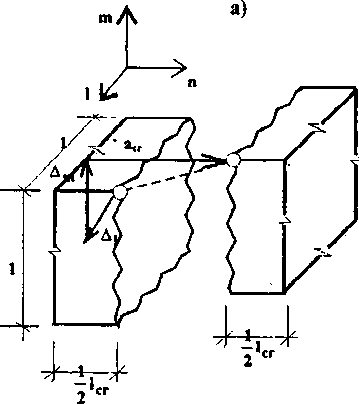
Деформации от раскрытия трещин и возможного сдвига их берегов определяются по схемам, показанным на рис. 7.8. Эти деформации составляют девятикомпонентный вектор-столбец, они также образуют несимметричный тензор второго ранга:
{ε*}n={εnεmεlg*nmg*mng*mlg*lmg*lng*nl} На основе данных предпосылок сначала устанавливается связь межу девятикомпонентными вектор-столбцами напряжений и деформаций
{σ*}n =[D*] {ε} n +{σ*0}, (7.9)
где [D*] - полностью заполненная симметричная матрица механических характеристик железобетона размером 9x9. Учитывая парность касательных-напряжений и вводя общие сдвиги типа 0,5grk =0,5(g*rk+g* rk), приходим к обычной связи между шестью компонентами напряжений {σ}л и деформаций {ε}л типа (2) и, естественно, к качественно иному
наполнению симметричной матрицы [D] размером 6x6 и вектора .
Таким образом, деформирование железобетона подобно деформированию физическинелинейного анизотропного материала с общим случаем анизотропии.
Представленные модели НИИЖБ были проверены при расчете многих опытных конструкций в работах бывших аспирантов и докторантов НИИЖБ (ныне докторов и кандидатов технических наук): А.Л. Гуревича, Л.И. Ярина, B.C. Кукунаева, Т.Д. Балана, А.Н. Петрова (расчет стен, плит, фрагментов зданий МКЭ и МКР), С.Ф. Клованича (расчет моделей реакторов при термосиловых воздействиях сосудов высокого давления),А.Я. Джанкулаева (расчет толстых плит) и др. Они также использованы при расчете и проектировании многих зданий из монолитного железобетона в г. Москве и других городах, а также отдельных конструкций (боль-шеразмерных монолитных плит, стен и ядер жесткости, фундаментных плит и др.).
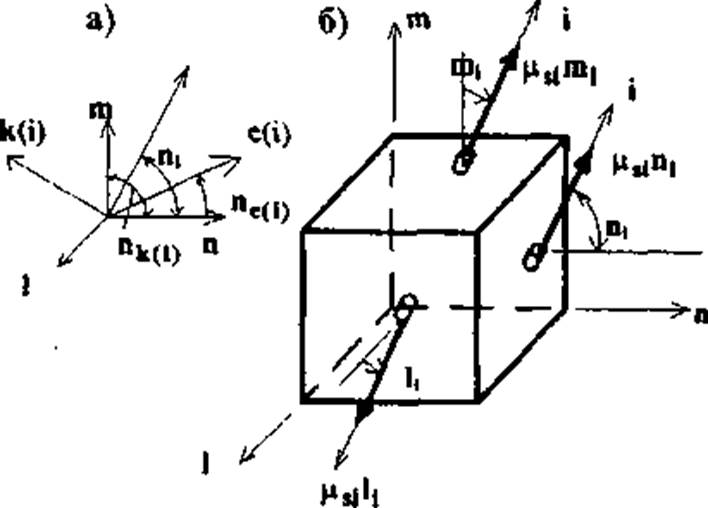 |
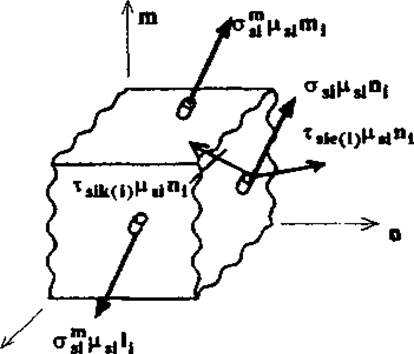
Рис.7.6. Напряжения в арматуре, пересекающей грани элемента
|
|
Рис. 7.7. Общие напряжения и их составляющие
 |
|||
 |
|||
Рис. 7.8. Деформации элемента с трещиной
массив
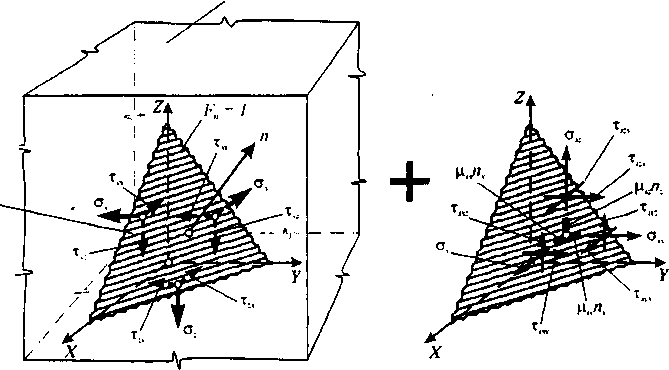
элементарный тетраэдр
Рис. 7.9. К определению напряжений в арматуре в трещинах элементарного объема массивной железобетонной конструкции.
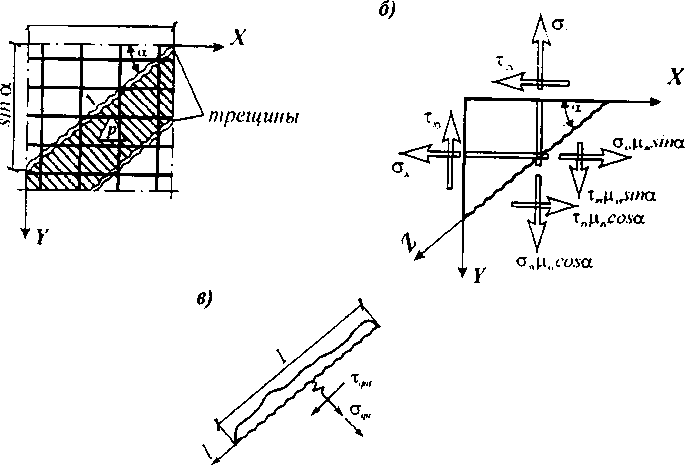 |
Рис. 7.10. К определению напряжений в арматуре в трещинах плоского элемента
а — плоский элемент с трещинами; б — нормальные и касательные напряжения в арматуре: в — влияние сил сцепления.
техники позволяет утверждать о реальных возможностях перехода к расчетам различных железобетонных конструкций и
сооружений с учетом физической нелинейности на уровне промышленных компьютерных программ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.