 |
|
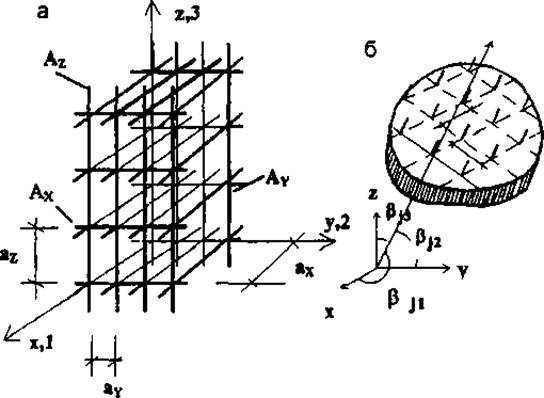
Рис.7. 2. Схемы армирования |
этой модели являются функциями главных напряжений или деформаций и их комбинаций. Ортотропная модель позволяет учитывать направленное развитие эффекта дилатации и неоднородность деформирования при сжатии и растяжении, и этим в большей степени отражает реальный характер деформаций бетона при плоском и объемном напряженном состоянии. Среди работ других исследователей, внесших вклад в развитие ортотропной модели, следует указать на работы А.С. Городецкого, B.C. Здоренко (И-ИАС, г. Киев), Т.Д. Балана, С.Ф. Клованича, Г.Р. Видного (ПИ, Кишинев), А.Н. Петрова (ПИ, Петрозаводск) и некоторых других (работы многих из этих исследователей начинались в лаборатории механики железобетона ГУП НИИЖБ).
Развитие теорий типа течения применительно к бетону также идет по пути учета нелинейности изменения объема и эффекта дилатации. При этом пластичность бетона уже нельзя ассоциировать с поверхностью текучести при помощи закона ортогональности и постулата Друкера. Неассоциированные формулировки развивались в работах В.М. Круглова и его учеников.
Современные теории течения для бетона еще находятся в стадии становления. В НИИЖБ это направление получило нетрадиционное развитие в виде разработки некоторой ортотропной модели бетона в приращениях. Развитие этого направления перспективно с позиции описания сложных режимов нагружения.
Анализируя в общем уровень развития моделей деформирования бетона, можно отметить, что, пожалуй, две первые модели (ортотропная модель и модифицированная модель малых упруго-пластических деформаций) уже достигли такого уровня разработки, что могут использоваться в нелинейных расчетных программах.
Модели деформирования железобетона с трещинами
В разработке этих наиболее сложных моделей исследователям НИИЖБ принадлежит, пожалуй, главенствующая роль. Исторически первой моделью деформирования железобетона является модель В.И. Мура-шева для изгибаемых элементов с трещинами, которая хорошо зарекомендовала себя при расчете балок, колонн, балочных плит. Однако, детальные экспериментальные исследования, выполненные в 1961 г. в НИИЖБ А.Н. Королевым и С.М. Крыловым под руководством А.А. Гвоздева над квадратными опертыми по контуру плитами при равномерной нагрузке, показали, что опытные прогибы значительно отклоняются отданных расчета по теории В.И. Мурашева (при этом, учитывая одинаковое армирование по двум направлениям, цилиндрическая жесткость заменялась на балочную жесткость по В.И. Мурашеву). Авторы предложили эмпирический путь определения прогибов, однако эти исследования дали значительный импульс к поиску новых построений. Были предложены несколько моделей деформирования железобетона с трещинами при неодноосном напряженном состоянии: анизотропная (работы Н.И. Карпенко по теории плит и стен с трещинами, начальные исследования выполнялись под руководством А.А. Гвоздева и С.М. Крылова); трансверсальноизотропная (работы ГА. Гениева и ГА. Тюпи-на); ортотропная (работы Я.Д. Лившица, М.М. Онищен-ко, В.Н. Байкова, Е.А. Палатникова по плитам, И.Е. Ми-лейковского по оболочкам и др.), где в основном корректировалась жесткость на кручение вплоть до равенства нулю (оси ортотропии совмещались с направлениями арматуры), а изгибаемые жесткости определялись по В.И. Мурашеву. Однако ортотропные модели не объясняли факт эффект значительного удлинения труб и их расширения по радиусу при частом кручении после образования трещин (опыты Э.Г. Елагина, выполненные в НИИЖБ под руководством Н.Н. Лессич), в то время как анизотропная модель позволила с хорошей точностью определить как углы закручивания, так и удлинение и расширение труб. В дальнейшем автором статьи был разработан общий случай анизотропной модели для объемного напряженного состояния. Влияние температурных деформаций учтено в работах Н.И. Карпенко и С.Ф. Клованича. Армирование характеризуется коэффициентами армирования μSiпо направлениям, диаметром стержней dSj и направляющими косинусами Uк выбранным осям i = х, у, z (рис. 7.2а,б). Выделяются два состояния работы элементов: без трещин и с трещинами. Для элементов без трещин общая матрица связи напряжений с деформациями [D] формируется в два этапа. Сначала в матрице бетонаучитываются два побочных фактора - влияние арматуры на сдвиг и на деформации в поперечном направлении по объемным коэффициентам содержания, а затем учитывается основной фактор - совместность осевых деформаций арматуры и бетона.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.