Критерии деформирования и разрушения железобетонных элементов. Общие модели деформирования бетона, страница 5

Напряжения в элементе являются составными, со­стоящими из напряжений в бетоне и приведенных на­пряжений в арматуре. В результате связь между на­пряжениями {σ} и деформациями {ε} принимает вид (при наличии начальных напряжений {σ₀}:

             {σ} = [D] {ε}+{σ₀}(7.8)

Полагается, что когда главные растягивающие на­пряжения в бетоне достигают предельных значений, найденных по условиям прочности, в нем образуются трещины. Вывод физических соотношений, устанавли­вающих связи между напряжениями и деформациями в железобетонном элементе с трещинами, является

наиболее важным в цепочке теоретических построений. При этом учитываются следующие факторы:

- углы наклона трещин к арматуре и схемы их пе­ресечения трещин (различаюттри схемы трещин, при­веденные на рис. 7.3);

- раскрытие трещин а_сг и сдвиг их берегов D(рис.7. 4);

-  жесткость арматуры при осевых деформациях (рис. 7.4,б) под действием напряжений в арматуре в зоне трещины с учетом влияния на деформации сил сцеп­ления арматуры с полосами и блоками бетона между трещинами (рис. 7.4,в);

- жесткость арматуры при тангенциальных пере­мещениях ее относительно берегов трещин под дей­ствием касательных напряжений в арматуре в зоне тре­щины с учетом

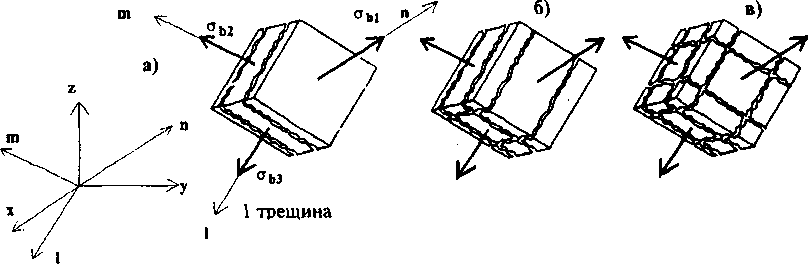                                                         2 трещина                          3 трещин

  Рис.7.3. схемы трещин

податливости бетонного основания у берегов трещины (рис. 7.4,г);

-   жесткость остаточных бетонных связей зацепле­ния берегов трещин при их сдвигах (обычно учитыва­ются в случае малой ширины раскрытия трещин);

-  нарушение совместности осевых деформаций арматуры и бетона между трещинами при сохранении условий совместности перемещений арматуры и бето­на в центре полос или блоков бетона между трещина­ми (в точке А рис. 7.3,в).

Напряжения в арматуре а трещинах определяются двояким способом - через средние деформации эле­мента (по схемам рис. 7.3 - рис. 7.8) или непосредственно через нормальные и касательные напряжения в эле­менте (по схемам рис. 7.9 - рис. 7.10). При этом трещины в общем случае располагаются наклонно к на­правлениям арматуры. Естественно, напряжения, пред­ставленные на рис. 7.9а и рис. 7.9б, в действительности совмещены на гранях одного тетраэдра (они разделя­ются лишь для удобства выкладок). Указанные схемы служат также для вывода критериев прочности (7.6)-(7.7) 

Указанные выше предпосылки не укладывались в традиционные пути построения физических соотноше­ний, используемых в композитных материалах, и тре­бовали новых подходов. Фактически необходимо было в малом элементе среды (условно в точке) иметь од­новременно два вида напряжений в каждом компонен­те (большие напряжения в арматуре в трещинах и прак­тически равные нулю напряжения в бетоне, и одновре­менно значительно меньшие напряжения в арматуре на площадках, нормальных к трещинам, и, наоборот, большие по модулю напряжения в бетоне на этих пло­щадках). В работах автора статьи эта проблема была решена на пути использования несимметричных тен­зоров напряжений для компонент арматуры и бетона (вводятся 9 компонент вместо 6 без соблюдения усло­вия парности касательных величин). Лишь в сумме сим­метричные компоненты становятся симметричными (с соблюдением парности касательных напряжений).