Расчет системы на устойчивость

СГТУ

БАЛАКОВСКИЙ  ИНСТИТУТ ТЕХНИКИ ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

КАФЕДРА УИТ

Лабораторная работа №1

Дисциплина: ЛСА

Вариант 29

Выполнил: студент

группы

УИТ-5в

Демин

Алексей

                                                                                  Проверил: преподаватель

                                                                                                       Скоробогатова

                                                                                                       Татьяна

                                                                                                       Николаевна

                                                                                  Принял:«__»_____»2001г.

2001г.

Задание №1

Задание:

          Рассчитать систему на устойчивость:

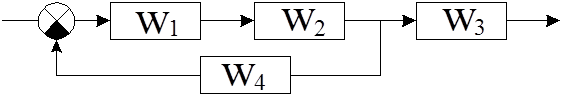
Где:     W₁=0,05;             W₁=0,05;             W₂=10⁵ ;              W₃=0,1p²+1;        W₄=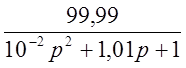

Методом:

1.  Ляпунова

2.  Рауса

3.  Гурвица

4.  Михайлова-Найквиста

5.  Льенара-Шипара

6.  Шур-Кона

Решение:

1.  Метод Ляпунова:

Рассчитаем передаточную функцию системы:

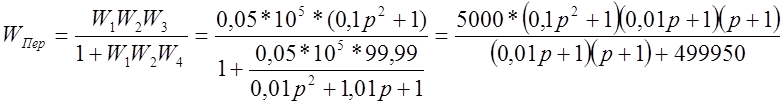
По методу Ляпунова решим характеристическое уравнение, приравнял его к нулю:

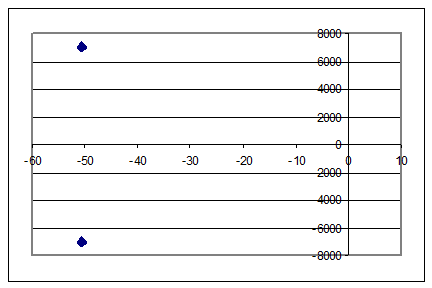
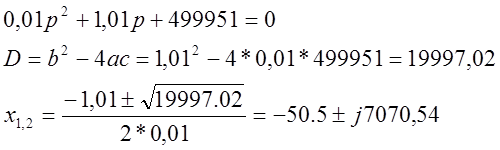
Корни уравнения на комплексной плоскости находятся в левой полуплоскости

Так как корни характеристического уравнения имеют отрицательные вещественные части, то реальная система устойчива и никакие отброшенные части 2 и 3 порядка не изменяют устойчивость системы. Так как присутствует комплексная составляющая, то существуют колебания системы. Значит система устойчива.

2.  Метод Рауса

По методу Рауса составим таблицу для характеристического уравнения замкнутой системы.

№ п.п.	с1	с2
1	499951	0,01
2	1,01	0
3	0,01

По 1 столбцу в таблице Рауса судим об устойчивости системы. Так как элементы столбца больше 0, то система устойчивая

3.  Метод Гурвица

Составим квадратную матрицу (n-n), где все n-определителей квадратных матриц должны быть больше 0.

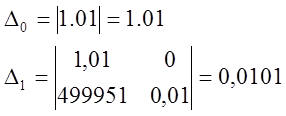
Так как все определители малых матриц больше 0. то значит система устойчивая.

4.  Критерий Михайлова-Найквиста.

Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова имел угол поворота 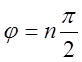 или годограф Найквиста не захватывал точку –1 на оси Х.

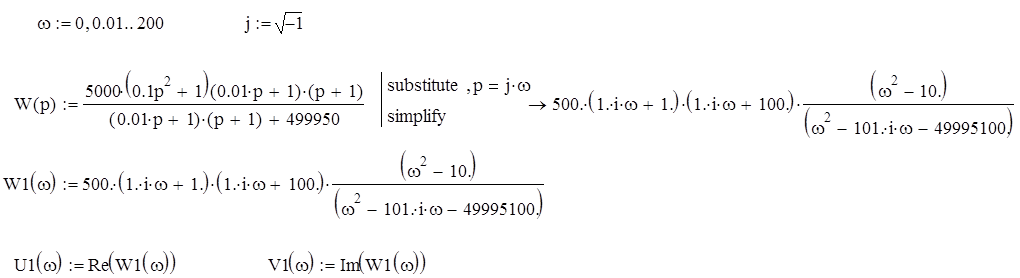
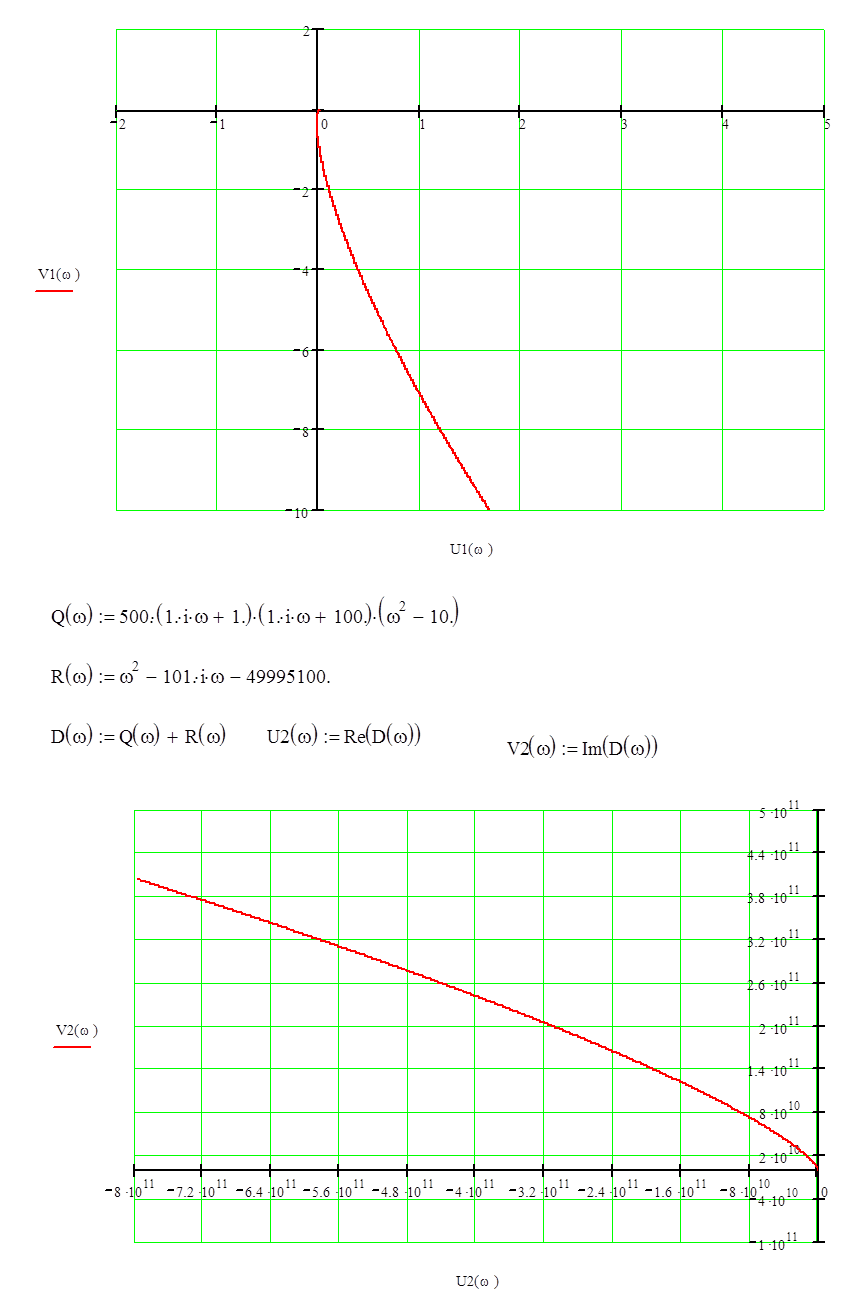
Так как у годографа Михайлова n=2 и степень характеристического полинома равна 2, и годограф Найквиста не захватил точку -1, то система является устойчивой.

5.  Д - разбиение.

Для устойчивости системы достаточно, чтобы функция Д - разбиения имела устойчивый график кривой.

Для этого выберем коэффициент в характеристическом уравнении у максимальной степени и решим относительного его уравнение  - Х(р).

Построим график функции данной системы.

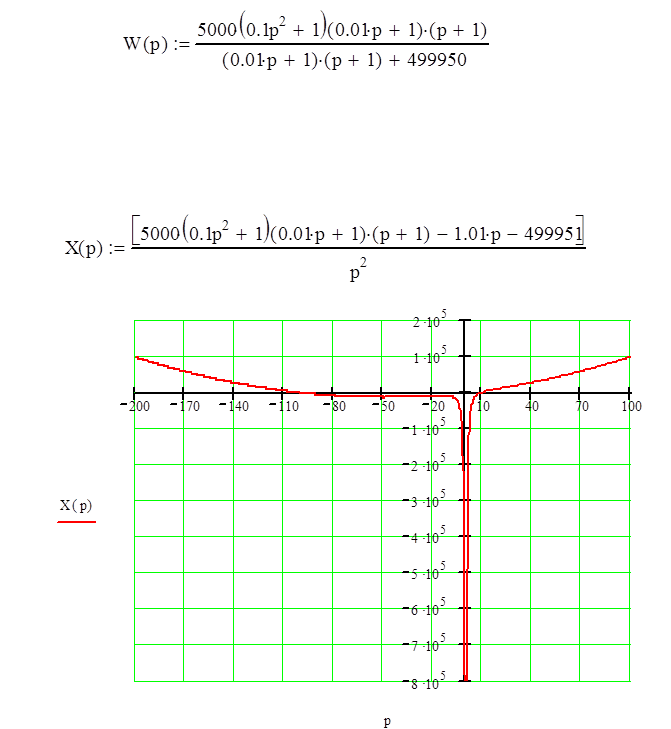
Из графика видно, что данная система является устойчивой.