Синтез САР. Последовательные корректирующие устройства

Синтез САР, основанный на построении желаемой логарифмической амплитудной и фазовой характеристик, полученных с помощью билинейного преобразования, состоит в следующем:

а) по требованиям точности (или коэффициентам добротностей) строим низкочастотную часть желаемой логарифмической амплитудной характеристики относительно псевдочастоты ω̄(H_ж (ω̄));

б) с помощью номограмм Солодовникова (рис. 9.4, б и в) по показателям качества σ_m и t_р находим частоту среза ω̄_с, через которую проводим логарифмическую амплитудную характеристику с наклоном – 20 дБ/дек;

в) строим во всем диапазоне псевдочастот логарифмическую характеристику неизменяемой части H_н (ω̄) проходящую через точку ω̄ = 1;

г) высокочастотную часть желаемой логарифмической амплитудной характеристики H_ж (ω̄) выбираем аналогичной H_н (ω̄);

д) по точкам излома H_ж (ω̄) вычисляем желаемую логарифмическую фазовую характеристику θ_ж (ω̄), которую наносим на полулогарифмическую бумагу, и определяем запасы устойчивости по фазе γ_Ф° и модулям ±H_М. Если они совпадают с данными технических условий, то построение желаемой характеристики на этом заканчивается. После этого можно приступить к формированию программ коррекции, реализуемых на микропроцессорах или микроЭВМ.

Рассмотрим применение данной методики для синтеза последовательных и параллельных корректирующих устройств.

Последовательные корректирующие устройства выбираем с использованием следующего соотношения:

H_кп (ω̄) = H_ж (ω̄) – H_н (ω̄).   (10.1)

Затем по логарифмической амплитудной характеристике H_кп (ω̄) находим W_кп (s̄) и, используя формулу (1.125), получим W_кп (z). Откуда и находим разностное уравнение, позволяющее реализовать программы коррекции.

Пример 10.1. Определить параметры системы, удовлетворяющей заданным техническим требованиям, и сформировать программу для микроЭВМ типа «Электроника-60», с помощью которой реализовано последовательное корректирующее устройство. Структурная схема системы изображена на рис. 10.1, а, где W₁ (s) = 1; W₂ (s) = W_н (s). Ее основные характеристики следующие: D_ω = 40 с ^{– 1}; D_ε = 7 с ^{– 2}; σ_m = 30%; t_р £ 3,14 с.

Непрерывная неизменяемая часть системы описывается с помощью передаточной функции вида

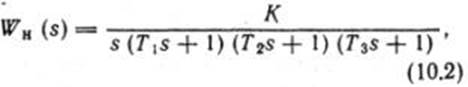
где K = 40 с ^{– 1}; Т₁ = 0,1 с; Т₂ = 0,05 с; Т₁ = 0,01 с.

Пусть такт обмена между непрерывной и дискретной частями T₀ £ 0,01 с. В этом случае на основании прил. П-I.2 запишем:

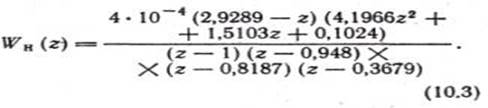
Подставляя в выражение (10.3)

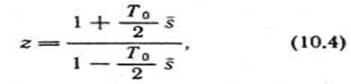
получим:

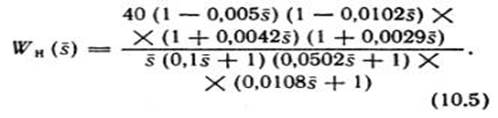
При s̄ = jω̄ из выражения (10.5) имеем:

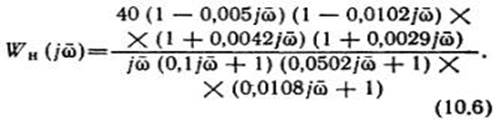
Характеристику H_н (ω̄) = 20 lg | W_н (jω̄) | проводим через точку ω̄ = 1 и наносим ее на рис. 10.2, а тонкой штриховой линией. Далее строим H_ж (ω̄) при D_ω = ω̄_к = 40 и D_ε = ω̄_l² = 7. По номограмме Солодовникова (рис. 9.4, б) найдем

ω̄_c = 4π/3,14 = 4.

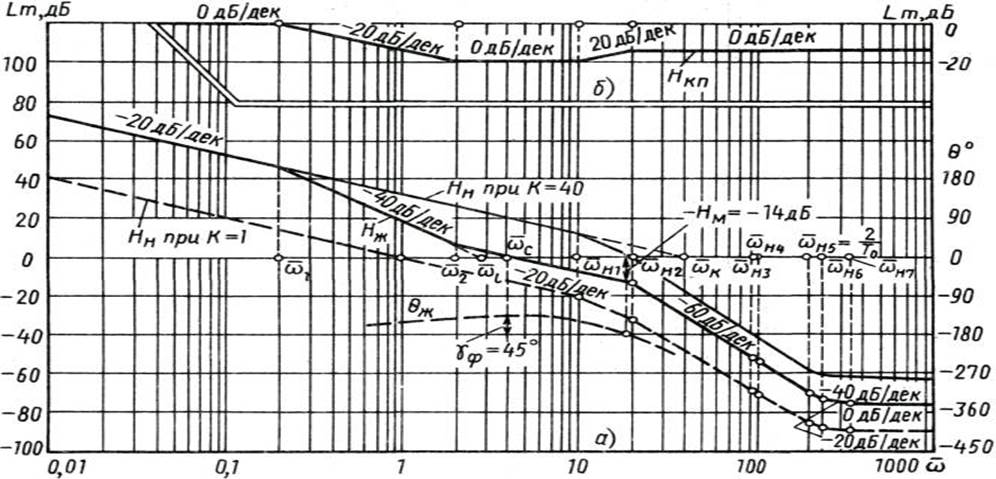
Рис. 10.2. Логарифмические амплитудные и фазовые характеристики дискретно-непрерывной системы с микроЭВМ «Электроника-60», на которой реализована последовательная программа коррекции:
а – всей системы и ее неизменяемой части;
б – для определения последовательной программы коррекции

Через точку ω̄_c на рис. 10.2, а проведем прямую с наклоном – 20 дБ/дек до второго излома H_н (ω̄). Затем достроим остальную часть желаемой логарифмической амплитудной частотной характеристики эквидистантно к высокочастотной части H_н (ω̄).

Располагая характеристикой H_ж (ω̄), запишем формулу для определения θ_ж (ω̄) в виде: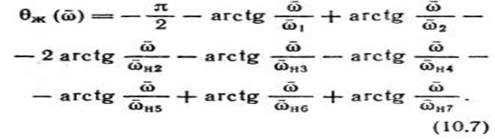

По формуле (10.7) в окрестности точки ω̄_c вычислим θ_ж (ω̄) и построим ее жирной штриховой линией на рис. 10.2, а, с помощью которой находим запасы устойчивости по фазе γ_Ф° = 45° и модулю – H_М = – 14 дБ. По номограмме (рис. 5.55) определим σ_m = 28 % и t_р = 2,8 с. Последние соответствуют требованиям технических условий.

Пользуясь формулой (10.1), строим H_кп (ωω̄) (рис. 10.2, б) и находим передаточную функцию последовательного корректирующего устройства:

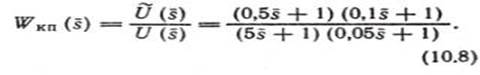
Подставляя в выражение (10.8) 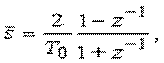получим:

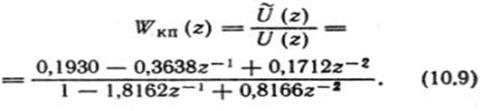
По формуле (10.9) найдем разностное уравнение в реальном масштабе времени, т.е. введя в числитель дополнительный сдвиг z ^{– 1}. В результате этого получим:

ũ_к = 1,8162 ũ_{к – 1} – 0,8166 ũ_{к – 2} + 0,1930 u_{к – 1} – 0,3638 u_{к – 2} + 0,1712 u_{к – 3}.  (10.10)

Реализуем программу коррекции на микроЭВМ «Электроника-60» на языке ассемблер.

Параллельные корректирующие устройства определяются в диапазоне ±26 дБ по аналогии с непрерывными системами, т.е.

H_{к пр} (ω̄) = – H_ж (ω̄).  (10.11)

Данная логарифмическая амплитудная характеристика справедлива для всего диапазона частот ω̄ при условии, что порядок астатизма исходной системы с выбранной коррекцией не понижается.

Пример 10.2. Синтезировать систему, удовлетворяющую заданным техническим требованиям, и сформировать программу для микроЭВМ типа «Электроника-60», на которой реализовано параллельное корректирующее устройство. Структурная схема системы изображена на рис. 10.1. б. Основные характеристики системы и ее неизменяемая часть соответствуют данным, приведенным в примере 10.1.

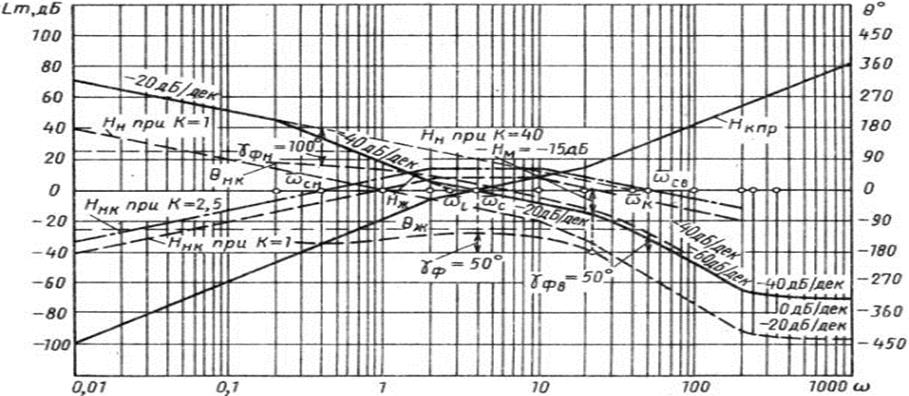
Рис. 10.3. Логарифмические амплитудные и фазовые характеристики дискретно-непрерывной системы с микроЭВМ «Электроника-60», на которой реализована параллельная программа коррекции

На рис. 10.3 изображены H_ж (ω̄) и θ_ж (ω̄). В отличие от ранее рассмотренного примера 10.1, желаемая амплитудная характеристика имеет дополнительный участок с наклоном – 40 дБ/дек в диапазоне 20 < ω̄ < 50. Запасы устойчивости синтезированной системы имеют следующие значения: γ_Ф° = 50° и – H_M = – 15 дБ. Жирной сплошной линией на рис. 10.3, согласно формуле (10.11), построена характеристика H_{к пр} (ω̄).

С целью проверки запасов устойчивости внутреннего контура на рис. 10.3 тонкой штриховой линией изображена характеристика H_нк (ω̄) = H_н (ω̄) + H_{к пр} (ω̄) при K = 1. По этой характеристике построена фазовая характеристика θ_нк (ω̄). Задаваясь запасом устойчивости по фазе γ_Фв° = 50° и поднимая H_нк (ω̄) до уровня K = 2,5, получим амплитудную характеристику внутреннего контура системы (штрихпунктирная линия). При этом видно, что γ_Фн° = 100°. Полученные значения γ_Фв° и γ_Фн° гарантируют высокую степень устойчивости замкнутого внутреннего контура.

Используя характеристику H_{к пр} (ω̄), находим передаточную функцию параллельного корректирующего устройства в виде:

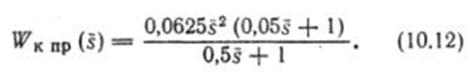
Подставляя в выражение (10.12) 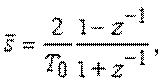получим:

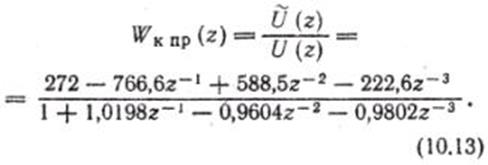
Соответствующее разностное уравнение в реальном масштабе времени имеет вид:

ũ_к = – 1,0198 ũ_{к – 1} + 0,9604 ũ_{к – 2} + 0,9802 ũ_{к – 3} + 272 u_{к – 1} – 766,6 u_{к – 2} + 588,5 u_{к – 3} – 222,6 u_{к – 4}.

(10.14)

Данное уравнение реализовано в виде программы на микроЭВМ «Электроника-60» на языке ассемблер.