Построение структурных схем для многомерных систем автоматического управления: Методические указания к выполнению практической работы

Апробация

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Саратовский государственный технический университет

Балаковский институт техники технологии и управления

ПОСТРОЕНИЕ СТРУКТУРНЫХ СХЕМ

ДЛЯ МНОГОМЕРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Методические указания к выполнению практической работы

по дисциплине «Математические основы теории систем»

для студентов специальности 210100

всех форм обучения

Одобрено

редакционно-издательским  советом

Балаковского института техники,

технологии и управления

Балаково 2009

ВВЕДЕНИЕ

Анализ многомерных систем управления является сложной задачей, так как при построении математической модели многомерной системы необходимо отследить воздействия, оказываемые на нее. На системы автоматического управления существует ряд воздействий. Входное – планируемое воздействие х(t). Возмущающее (внешнее) воздействие  f(t), примером такого возмущения может служить воздействие на систему окружающей среды. Внутреннее воздействие z(t)- воздействие, оказываемое одним элементом системы на другой. Выходное воздействие y(t).

Для более удобного описания системы методами теории математического управления, систему разбивают на элементы – звенья. Для каждого звена составляют дифференциальное уравнение, в предположении, что пока звено не связано с остальными звеньями. Затем, к получившимся математическим описаниям звеньев добавляют уравнение связи между звеньями, то есть общая модель состоит из 2 составляющих -  модели звеньев и уравнений связи между звеньями. Также моделью системы можно  считать структурную схему, где все воздействия на систему представлены в виде сигналов, а параметры системы представлены в виде звеньев с соответствующими передаточными функциями.

ЦЕЛЬ РАБОТЫ.  Ознакомиться с принципами построения структурных схем для многомерных систем  или объектов управления, заданных системой уравнений.

ОСНОВНЫЕ ПОНЯТИЯ

Многомерная система – это система, которая независимо от количества входов имеет несколько выходных величин. Для многомерных систем входные, выходные и внутренние параметры систем являются векторными величинами. Так, например, существует множество входных переменных , множество выходных переменных . Порядок переменных строго задан и учитывается в расчетах. 

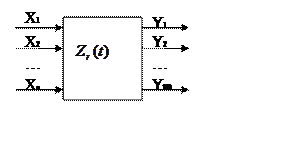Общий вид многомерной САУ представлен на рис.1.

Рис.1. Многомерная САУ

Для многомерной САУ входной, выходной сигнал и внутреннее состояние будет описываться векторами вида 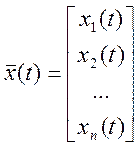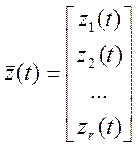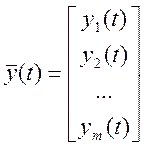(1).

; ;                           (1)

В общем случае многомерные системы можно описать с помощью системы дифференциальных уравнений вида 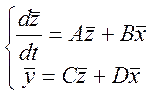(2):

                                                        (2)

где А – матрица, которая состоит из коэффициентов a_i,j, имеющая размерность r´r, (где r – количество внутренних воздействий на систему) и определяет коэффициенты при Z в уравнении, описывающем внутреннее состояние объекта. Матрица B – состоит из коэффициентов b_i,_j имеет размерность r´n (n – количество входных воздействий на систему) и определяет коэффициенты при входных параметрах в уравнении, описывающем внутреннее состояние объекта. Матрица С – состоит из коэффициентов с_i,_j , размерностью m´r  (m – количество выходных параметров системы) и определяет коэффициенты при Z в уравнении для выходной величины. Матрица D – состоит из коэффициентов d_i,_j , размерностью m´n и определяет коэффициентыпри входных параметрах в уравнениях для выходной величины.

Если система является одномерной и имеет один вход и один выход система (2) преобразуя к виду:

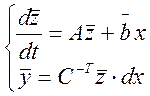
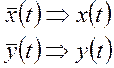                                                                  (3)

В этом случае вектору входных и выходных переменных соответствуют скалярные функции x(t) и y(t). Матрица B заменяется вектором столбцом . Матрица С преобразуется в транспонированную матрицу . Матрица D представляет собой скаляр  d. Наличие в системе производной означает, что выходной сигнал системы зависит от входного не только в текущий момент времени, но и от его значения в предыдущие моменты времени.

ПРАВИЛА СОСТАВЛЕНИЯ СТРУКТУРНЫХ СХЕМ

Структурная схема многомерных САУ строится в соответствие  с правилами составления структурных схем, описанным в /1,2/. При построении структурной схемы должны выполняться следующие правила:

- входное воздействие располагается в левой части схемы,  выходная величина – в правой;

- производные от внутреннего состояния системы изображается в виде сумматора;

- переход от производной к переменной осуществляется с помощью интегрирующего звена первого порядка (интегратора) с передаточной функцией 1/р. При этом после перехода внутреннее состояние изображается на схеме в виде узла;

- все элементы матриц отображаются на структурной схеме звеном с передаточной функцией равной коэффициенту соответствующей матрицы.

- наддиагональные элементы матрицы А характеризуют передачу сигнала по прямой цепи связи;