









Балаковский институт техники, технологии и управления
ИТЕРАЦИОННЫЕ МЕТОДЫ И СИМВОЛЬНОЕ РЕШЕНИЕ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ САУ СРЕДСТВАМИ MATHCAD
Методические указания к выполнению контрольной работы
по дисциплине «Математические основы теории систем»
для студентов специальности 220
201 «Управление и информатика в технических системах»
заочной формы обучения
Одобрено
редакционно-издательским советом
Балаковского института техники,
технологии и управления
Балаково 2010
ВВЕДЕНИЕ
Многие системы автоматического управления описываются нелинейными уравнениями или системой уравнений, которые не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы найти аналитическое решение математической модели САУ, которая описывается уравнением степени выше четвертой. Однако такие математические модели могут решаться итерационными методами с заданной точностью.
Задача нахождения корня уравнения f(x) = 0 итерационными методами состоит в следующем:
- отделение корней - отыскание приближенного значения корня (например, графическим методом);
- уточнение корней - доведение их значений до заданной степени точности.
Цель работы: научиться применять итерационные методы для поиска решения математических моделей систем автоматического управления с применением современных программных продуктов.
УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАБОТЫ
Метод Ньютона
Существует несколько приближенных методов решения нелинейных уравнений. Рассмотрим подробнее метод Ньютона: метод простых итераций. При использовании метода Ньютона необходимо задаться начальным приближением х0, расположенным достаточно близко к точному значению корня. Для этого по заданной функции f(x), на заданном интервале, в программной среде строится график функции в декартовой системе координат и визуально, по графику определяется значение аргумента х0 при котором функция f(x)=0. Далее необходимо задать предположительное число итераций n, обозначить шаг итераций i=0..n и точность вычислений e.
Согласно методу Ньютона, следует провести вычисление первого приближения по формуле:
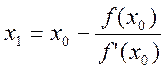 , (1)
, (1)
где f’(x0) – производная функции f(x) при конкретном значении аргумента.
При нахождении производной должно выполняться равенство:
![]() (2)
(2)
Функция Mathcad until возвращает аргумент х до тех пор, пока функция не примет отрицательное значение. Далее итерационный процесс строится по формуле:
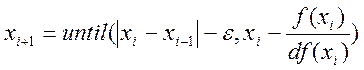 , (3)
, (3)
где e - точность вычислений;
хi-1 –значение аргумента на предыдущем шаге итерации;
хi+1 – значение аргумента на последующем шаге итерации.
Достаточным условием сходимости итерационных процессов является выполнение неравенства (4) на каждом шаге итерации.
![]() (4)
(4)
После проведенных расчетов необходимо определить число итераций, за которые сошелся итерационный процесс. Выполняется это в Mathcad при помощи функции last (x) в скобках указывается аргумент функции.
Решение уравнений средствами Mathcad
Для простейших уравнений вида f(x) = 0 решение находится с помощью функции root. Root (f(х);х) - возвращает значение х, при котором выражение или функция f(х) обращается в ноль. Оба аргумента этой функции должны быть скалярами. Первый аргумент или функция, определенная где-либо в рабочем документе, или выражение. Второй аргумент - имя переменной, которая используется в выражении. Этой переменной перед использованием функции root необходимо присвоить числовое значение.
Для нахождения корней выражения, имеющего вид (5), лучше использовать функцию polyroots.
![]() (5)
(5)
В отличие от функции root, функция polyrootsне требует начального приближения и возвращает сразу все корни как вещественные, так и комплексные. Рolyroots (V) возвращает корни полинома степени n. Коэффициенты полинома находятся в векторе V длины n + 1. Также уравнение вида f(x)=0 можно решить в Mathcad при помощи функции solveи традиционными способами, разложив функцию на множители при помощи функции Mathcad factor .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.