Вариант №21
 Дано: L1 e(t) e1(t)
Дано: L1 e(t) e1(t)
i2 i1 i3 i4 C2
R1 R2 R6
R3 R4 L4
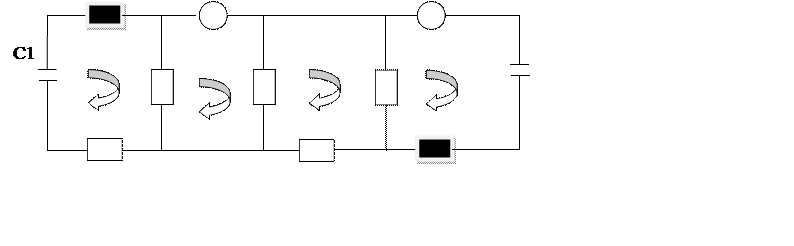
Рис. 1. Эквивалентная схема объекта управления
R1 =343 Ом
R2=361 Ом
R3=124 Ом
R4=202 Ом
R6=268 Ом
L4=21 Гн
L1=31 Гн
C1=39564*10-6 Ф
С2=26536*10-6 Ф
i2= ?
ПЕРВАЯ ЧАСТЬ
1.Построить математическую модель объекта управления в пространстве состояния.
Структурная схема объекта управления:
![]()
![]()
|
е i2
Рис. 2. Структрная схема объекта управления
В схеме четыре элемента запасающих энергию: L1, L4, C1, C2 следовательно, математическая модель четвёртого порядка.
Задаём направление контурных токов i1, i2, i3, i4, и составляем четыре уравнения по 2-му закону Кирхгоффа для контуров:
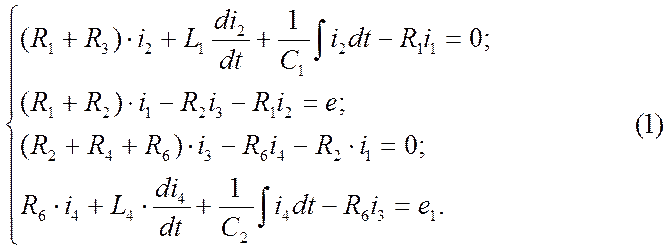
В 1 и 4 уравнениях системы есть интегралы, продифференцируем их:
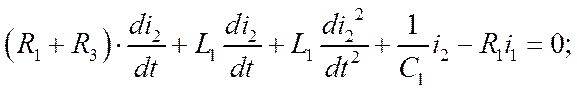 (1.1*)
(1.1*)
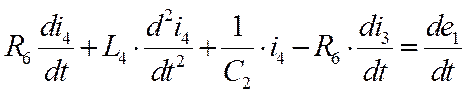 (1.4*)
(1.4*)
В уравнениях (1.1*) ,(1.4*), 1.4, 1.3, 1.2 есть производные, в качестве X1 X2 X3 X4 выбираем элементы производными и производные берём на порядок ниже.
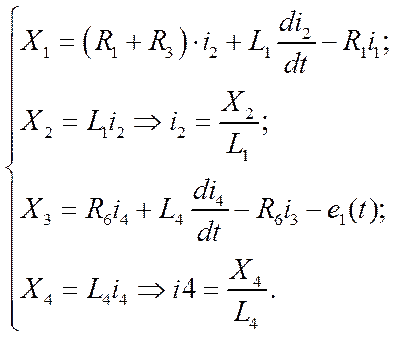 (2)
(2)
Запишем введённый вектор состояния в виде диф. уравнения первого порядка и уравнения в пространстве состояний:
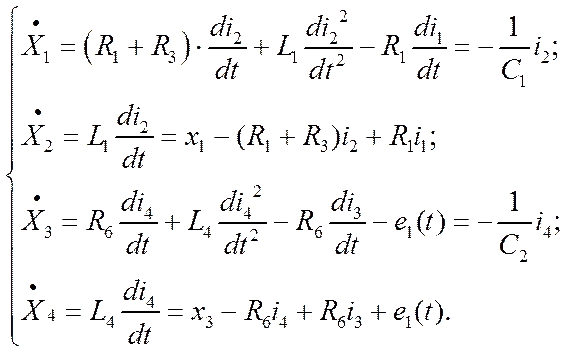 (3)
(3)
В полученных уравнениях имеется 8 переменных: i1, i2, i3, i4, x1, x2, x3, x4.
Надо уйти от i1, i2, i3, i4 выразив их через x1, x2, x3, x4.
Выразим i1 из (1):
![]()
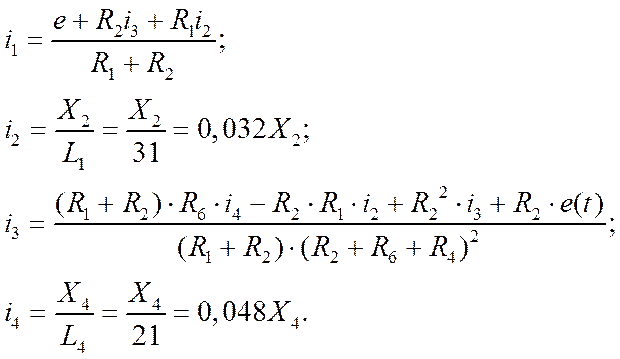
![]()
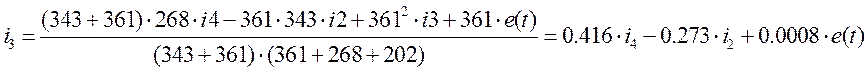
![]()
![]()
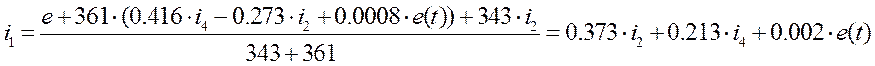
Находим x1, x2, x3, x4 из (3)
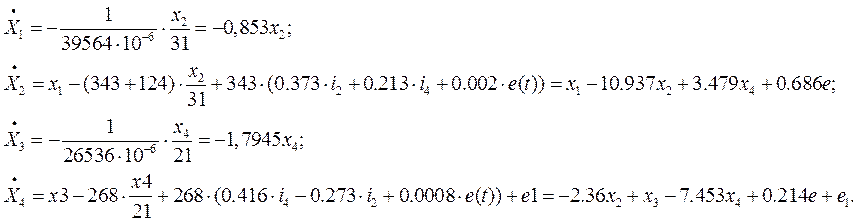
Получим четыре диф. уравнения и одно для выходного параметра.
Запишем полученную систему в матричном виде:
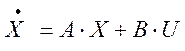
X= ![]() A=
A=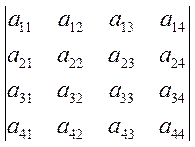 B=
B=![]()
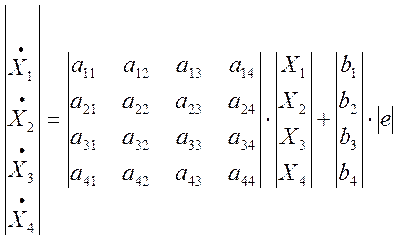
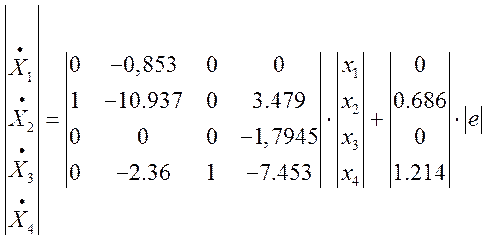
Получим матричное уравнение для выходной переменной
![]()
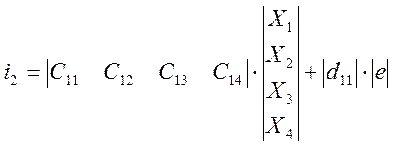
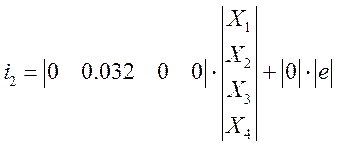
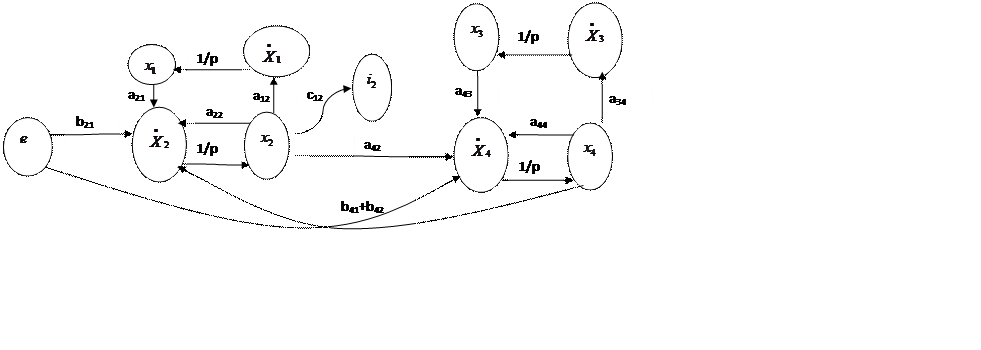
2. Построение сигнального графа и структурной схемы системы.
Перепишем уравнения в общем виде для построения графа системы.
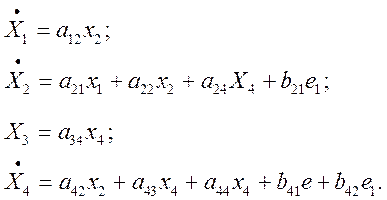
|
|
Рис. 3. Граф системы.
Построим структурную схему:
Рис 4. Структурная схема системы
Определим вид передаточной функции ОУ используя формулу Мейсона:
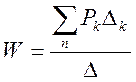 (4)
(4)
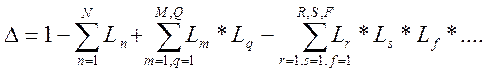
где к - количество возможных прямых путей от входа к выходу;
∆ - определитель графа;
Рk - коэффициент передачи кого пути от входа к выходу;
∆к - определитель всех касающихся контуров при удалении кого пути;
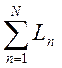 - сумма коэффициентов передачи всех отдельных контуров;
- сумма коэффициентов передачи всех отдельных контуров;
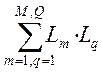 - сумма всех возможных произведений из 2ух
некасающихся контуров;
- сумма всех возможных произведений из 2ух
некасающихся контуров;
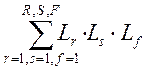 - сумма всех
возможных комбинаций из 3ёх не касающихся контуров.
- сумма всех
возможных комбинаций из 3ёх не касающихся контуров.
Определим прямые пути и запишем их уравнения:
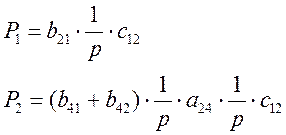
Определим все замкнутые контура и запишем их уравнения:
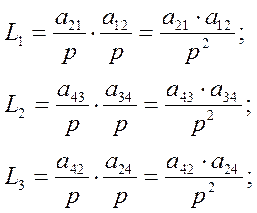
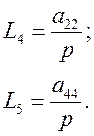
Запишем уравнения для определителя графа:
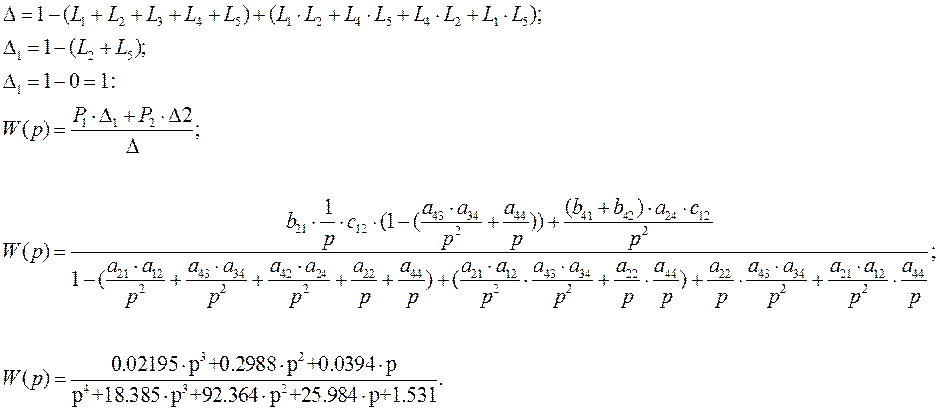
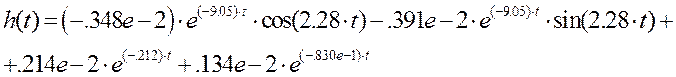
Построим график переходной функции:
|
Рис. 5. График переходной функции |
Определим импульсную функцию системы:
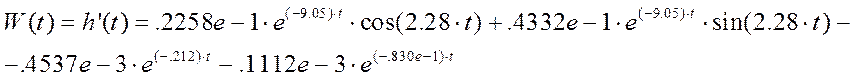
|
Рис. 6. График импульсной функции |
Частотная функция системы выразится следующим образом:
|
|
Определим АЧХ и ФЧХ и построим их графики:
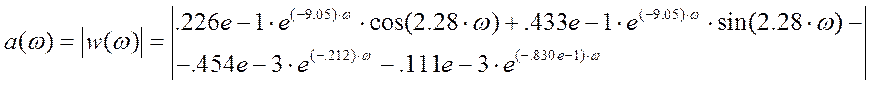
|
Рис. 7. График АЧХ |
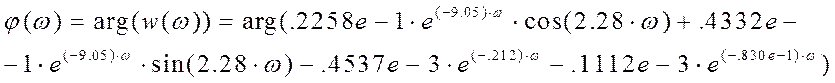
|
Рис. 8. График ФЧХ |
Определим прямые и косвенные оценки качества ОУ по полученным зависимостям
По графику h(t) произведем прямую оценку качества системы
Время переходного процесса tперех.=50 с.
Перерегулирование 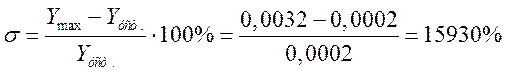
Колебательность n=0.
Время нарастания регулируемой величины tнар.=0,5 с.
Время первого согласования tсог.=59 с.
По графику АЧХ видно, что система является неустойчивой, поэтому косвенную оценку качества проводить в данном случае неуместно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.