Исследование цифровых систем методом логарифмических частотных характеристик.
Метод ЛЧХ может быть разработан на основе υ-преобразования, который заключатся в замене передаточной функции дискретной системы W(z), полученной путем z-преобразования, функцией W(υ), c помощью подстановки
z=(1+ υ)/(1- υ) или υ=(z-1)/(z+1).
Рассмотрим его более подробно, для чего запишем его в виде υ=(epT-1)/ (epT+1)
Полагая pT=jω*, получаем
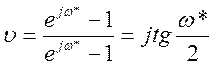
Так как правая часть данного равенства – мнимая величина, то и левая часть будет мнимой величиной. Вводя обозначение υ=jλ*, получим
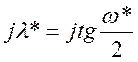
откуда
![]()
При изменении ω* от 0 до π значения λ* изменяются от 0 до ∞. Так как ω*= ωT, то имеет место также соотношение:
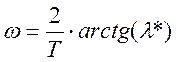
Переменную λ* называют безразмерной псевдочастотой. Однако при исследовании дискретных систем в ряде случаев более удобна размерная псевдочастота λ, которую введем с помощью соответствия
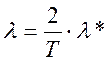 .
.
Принимая во внимание это равенство, получаем формулу от реальной к псевдочастоте.
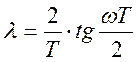
Откуда следует, что при изменении ω от 0 до π/T псевдочастота λ принимает значение
0 < λ [c-1] < ∞. Далее будем пользоваться υ-преобразованием, связанным с размерной псевдочастотой и записанным в виде соотношения:
![]()
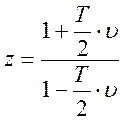 ,
, ![]()
Если теперь в передаточную функцию W(z) ввести переменную υ, то получим записанную через υ-преобразование передаточную функцию разомкнутой дискретной системы W(υ). Которая позволяет использовать для анализа и синтеза цифровых систем логарифмические частотные характеристики. При этом ЛЧХ, соответствующие частотной характеристике W(jλ), определяются теми же соотношениями, что и для обычных непрерывных систем.
![]()
![]()
![]()
Таким образом,
после проведения соответствующих преобразований, синтез дискретного
корректирующего устройства может проводиться методом Солодовникова или методом
запретной зоны. Затем полученную передаточную функцию корректирующего
устройства Wk(jλ) = Wк(υ) требуется преобразовать к виду Wk(z) путем
замены 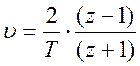
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.