Исследование устойчивости систем автоматического регулирования: Методические указания к выполнению лабораторной работы

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ систем

автоматического регулирования

Методические указания для студентов

специальностей:

210100 (код 65) - Управление и информатика в технических системах;

080507 (код 65)  – Менеджмент организации;

080801 (код 65) – Прикладная информатика (в автомобилях и  автомобильном хозяйстве).

Балаково 2007

ЦЕЛЬ РАБОТЫ: изучить методы исследования устойчивости ста­ционарных и нестационарных линейных непрерывных и дискретно-непрерывных САР.

ОСНОВНЫЕ ПОНЯТИЯ

Понятия устойчивости стационарных и нестационарных линейных непрерывных и дискретно-непрерывных САР существенно различаются. Для случая стационарных систем необходимым и достаточным условием устойчивости следует считать такое, когда единственным положением равновесия будет начало координат, если характеристическое уравнение не имеет полюсов ни в правой части комплексной плоскости, ни на мни­мой оси при входном сигнале, равном нулю. Сразу же отметим, что для определения устойчивости систем нет необходимости вычислять корни характеристического уравнения. Необходимо только знать, как они распо­лагаются на комплексной плоскости. Для этого существуют некоторые правила, называемые критериями устойчивости.

В нестационарных системах изменение параметров может привести к нарушению сформулированного условия устойчивости стационарных систем; так, в характеристическом уравнении могут появиться полюсы как в правой полуплоскости, так и на мнимой оси. Поэтому при использовании критериев устойчивости приходится накладывать дополнительные ограни­чения.

1. Устойчивость систем по методу Ляпунова

В общем случае уравнение динамики замкнутых линейных стационарных САР будет:   

 Для этой системы при постоянном управляющем воздействии g (t) и наличии матрицы обратной Аз, положение равновесия находится в точке , где g(t) равно постоянной величине r. Когда управляю­щее воздействие g(t) зависит от времени, то в общем случае не представляется возможным найти такое преобразование, которое определяло бы единственное положение равновесия. Тогда исследование устойчивости линейных систем по методу Ляпунова нельзя переносить непосредственно на системы с произвольным входным воздействием. Сначала рассмотрим автономные линейные стационарные замкнутые системы.  

Линейную непрерывную автономную стационарную систему мож­но описать уравнением:

                                                                         (1)

Представим функцию Ляпунова в векторно-матричном виде
                                           

где

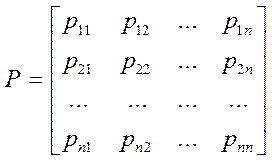                                                         (3)

или в обычной квадратичной форме

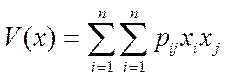                                                                (4)

где - постоянные коэффициенты.

Квадратичная форма (3) будет положительно – определенной, если каждый из ее главных угловых миноров удовлетворяет условиям:

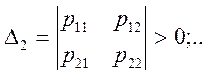
Пример. Допустим, что функция Ляпунова Имеет вид

тогда ее квадратичная форма

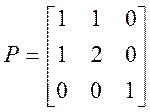
При этом миноры

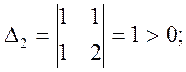
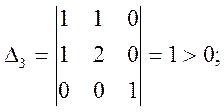
Все они положительны, значит, квадратичная форма положительно определена.

Пользуясь выражением (2) можно установить, что матрица Р будет положительно-определенной при  и отрицательно- определенной, когда  знакоположительной, если

Существуют признаки, с помощью которых можно проверить каким из указанных выше свойств обладает матрица Р. Для этого необходимо найти собственные значения  как решение характеристического уравнения

                                                     (5)

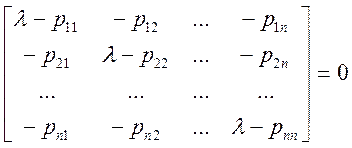или                                    (6)

Матрица Р положительно-определенна, если собственные значения  положительны; отрицательно-определена, если  отрицательны; знакоположительна и знакоотрицательна, если  имеют разные знаки, и неопределенна, если

Определим производную от функции V(x), которая была записана в виде

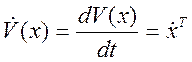
В уравнении (7) введем следующее обозначение:

Сформулируем основное положение об асимптотической устойчивости Ляпунова.

При положительно-определенной матрице   и V>0 в некоторой области , включающей в себя начало координат, положение равновесия в начале координат будет асимптотически устойчиво.

При анализе устойчивости линейных автономных систем используется также способ, связанный с исследованием корней характеристического уравнения матрицы Аз.

Обозначим корни характеристического уравнения через  тогда

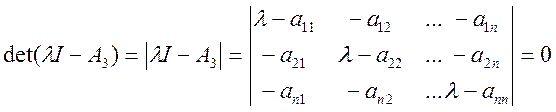    (8)

Раскрыв определитель (8), получим

                      (9)

При исследовании устойчивости в ряде случаев можно использовать уравнение

                                (10)