Так як за умовою похідна функції ![]() має з
нею протилежний знак
має з
нею протилежний знак 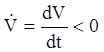 , то функція
, то функція ![]() при
при ![]() уздовж
траєкторії не зростає. Тому
уздовж
траєкторії не зростає. Тому
![]() .
.
З іншого боку, тому що точка ![]() належить сфері
належить сфері ![]() , то
, то ![]() , що
суперечить попередній.
, що
суперечить попередній.
Виходить, траєкторія поточної точки ![]() не
виходить за межі кулі
не
виходить за межі кулі ![]() й рух системи стійкий.
й рух системи стійкий.
Теорема 2. Якщо
диференціальні рівняння обуреного руху такі, що можна знайти знаковизначену
функцію ![]() , похідна
, похідна ![]() якої в
силу цих умов була б теж знаковизначеною функцією, але протилежного з
якої в
силу цих умов була б теж знаковизначеною функцією, але протилежного з ![]() знака, то незбурений рух асимптотичне
стійкий.
знака, то незбурений рух асимптотичне
стійкий.
Доведення. У
відмінності від попередньої теореми ![]() й може звертатися в
нуль тільки на початку координат. Тому в цьому випадку точка, відразу ж після
початку руху входить усередину
й може звертатися в
нуль тільки на початку координат. Тому в цьому випадку точка, відразу ж після
початку руху входить усередину ![]() кривій. Припускаючи
функцію
кривій. Припускаючи
функцію ![]() обумовлено-додатною, одержуємо за умовою
теореми
обумовлено-додатною, одержуємо за умовою
теореми ![]() , звідки маємо, що функція
, звідки маємо, що функція ![]() монотонно убуває, будучи обмеженою функцією
монотонно убуває, будучи обмеженою функцією
![]() . А це значить, що при
. А це значить, що при ![]() функція
функція ![]() прагне
до деякої межі
прагне
до деякої межі ![]() , тобто точка
, тобто точка ![]() , прагне із зовнішньої сторони до деякої
граничної
, прагне із зовнішньої сторони до деякої
граничної ![]() кривої . Покажемо, що
кривої . Покажемо, що ![]() . Доведемо від супротивного. Нехай
. Доведемо від супротивного. Нехай ![]() , а
, а ![]() -
найбільше від’ємне значення функції
-
найбільше від’ємне значення функції ![]() в замкнутій області між
кривими
в замкнутій області між
кривими ![]() й
й ![]() . Тоді в
зазначеній області має місце оцінка
. Тоді в
зазначеній області має місце оцінка
![]() .
.
Тоді, з огляду на останню нерівність, одержуємо
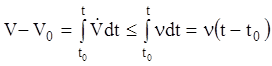 ,
,
де ![]() -
значення функції
-
значення функції ![]() при
при ![]() . З
останнього співвідношення одержуємо
. З
останнього співвідношення одержуємо
![]() .
.
Так як ![]() , то, починаючи з деякого
, то, починаючи з деякого ![]() функція
функція ![]() стане
від’ємною, що суперечить умові обумовлено-додатної функції
стане
від’ємною, що суперечить умові обумовлено-додатної функції ![]() . Значить допущення
. Значить допущення ![]() невірно,
тоді
невірно,
тоді ![]() . Таким чином, точка
. Таким чином, точка ![]() при
при ![]() прагне
до нуля, звідки витікає асимптотична стійкість незбуреного руху.
прагне
до нуля, звідки витікає асимптотична стійкість незбуреного руху.
Теорема 3 (Четаєва). Якщо
для системи (3.56) існує функція ![]() для
якої в як завгодно малої околиці точки спокою при
для
якої в як завгодно малої околиці точки спокою при ![]() існує
область
існує
область ![]() і функція
і функція ![]() в цій
області обмежена, а її похідна
в цій
області обмежена, а її похідна 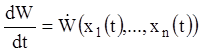 в силу системи (3.56)
додатна, причому в області, де
в силу системи (3.56)
додатна, причому в області, де ![]() ,
, ![]() , то точка спокою системи нестійка.
, то точка спокою системи нестійка.
Доведення. Розглянемо
коло ![]() , що містить область
, що містить область ![]() , а в колі
, а в колі ![]() точку
точку ![]() , у якій
, у якій ![]() .
Розглянемо деяку траєкторію
.
Розглянемо деяку траєкторію ![]() або поточну точку
або поточну точку ![]() , що починається в точці
, що починається в точці ![]() і покажемо, що в деякий момент часу
і покажемо, що в деякий момент часу ![]() поточна точка
поточна точка ![]() потрапить
на границю кола
потрапить
на границю кола ![]() .
.
Якщо покласти протилежне, що поточна точка ![]() траєкторії
при
траєкторії
при ![]() не вийде за межі
не вийде за межі ![]() ,
то будемо мати нерівність
,
то будемо мати нерівність ![]() , а, значить і
нерівність
, а, значить і
нерівність ![]() , що суперечить умові обмеженості функції W
в області
, що суперечить умові обмеженості функції W
в області ![]() :
:
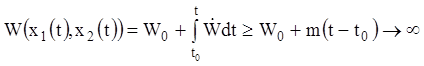 при
при ![]()
отримане протиріччя показує,
що в будь-якій околиці точки спокою існує траєкторія ![]() ,
що при
,
що при ![]() виходить за межі кола
виходить за межі кола ![]() . Виходить, точка спокою системи нестійка.
. Виходить, точка спокою системи нестійка.
Коментарі до теорем. Для нестійкості системи
досить установити, що вона має хоча б одну траєкторію, що бере початок в ![]() - околиці точки спокою й необмежено зростає
при
- околиці точки спокою й необмежено зростає
при ![]() ,
, ![]() . Під
функціями
. Під
функціями ![]() розуміють такі функції, які дорівнюють
нулю не тільки в точці спокою, а й на деяких необмежених поверхнях
розуміють такі функції, які дорівнюють
нулю не тільки в точці спокою, а й на деяких необмежених поверхнях ![]() , які проходять через цю точку, причому
хоча б в одній області, обмеженої двома такими поверхнями
, які проходять через цю точку, причому
хоча б в одній області, обмеженої двома такими поверхнями ![]() при
при ![]() . Такою
є в теоремі область
. Такою
є в теоремі область ![]() .
.
Розглянуті вище теореми показують, що вирішальну роль у справі
дослідження руху систем на стійкість грають функції ![]() або
або![]() , які в силу рівнянь збуреного руху повинні
мати деякі певні властивості. Однак ці теореми не вказують методу побудови цих
функцій. Відзначимо, що не існує загального методу побудови функцій Ляпунова
(хоча для цієї мети й існують деякі прийоми, застосовувані в окремих випадках)
і успіх на цьому шляху забезпечується тільки дотепністю й досвідом дослідника.
, які в силу рівнянь збуреного руху повинні
мати деякі певні властивості. Однак ці теореми не вказують методу побудови цих
функцій. Відзначимо, що не існує загального методу побудови функцій Ляпунова
(хоча для цієї мети й існують деякі прийоми, застосовувані в окремих випадках)
і успіх на цьому шляху забезпечується тільки дотепністю й досвідом дослідника.
У найпростіших випадках функцію Ляпунова можна шукати у вигляді
![]() ,
, ![]() ,
,
![]()
![]() і
т.д.
і
т.д.
Розглянемо деякі приклади.
Приклад 1. Дослідити стійкість системи
![]() ,
, ![]() .
.
Розв’язання. Рівняння першого наближення не дозволили нам відповістити
на запитання про стійкість нульового розв'язання системи. Побудуємо функцію Ляпунова
у вигляді ![]() , що є додатньо-визначеною. Використовуючи
рівняння збуреного руху, обчислюємо повну похідну функції Ляпунова
, що є додатньо-визначеною. Використовуючи
рівняння збуреного руху, обчислюємо повну похідну функції Ляпунова
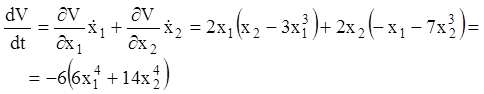 .
.
Tак
як похідна ![]() виявляється обумовлено-від’ємною функцією,
то на підставі теореми 2 робимо висновок, що нульове розв'язання асимптотично
стійке.
виявляється обумовлено-від’ємною функцією,
то на підставі теореми 2 робимо висновок, що нульове розв'язання асимптотично
стійке.
Приклад 2. Дослідити стійкість системи.
![]() ,
, ![]() .
.
Розв’язання. Візьмемо як функція Ляпунова безперечно додатна функцію 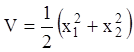 . Обчислимо повну похідну
. Обчислимо повну похідну
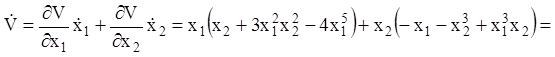
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.