Особливо корисно це твердження у випадку ![]() . Тоді
крива
. Тоді
крива ![]() замкнута й містить усередині себе початок
координат. Ми доведемо це твердження, якщо покажемо, що будь-яка неперервна
крива
замкнута й містить усередині себе початок
координат. Ми доведемо це твердження, якщо покажемо, що будь-яка неперервна
крива ![]() , що виходить із початку координат
, що виходить із початку координат ![]() і йде до якої-небудь точки
і йде до якої-небудь точки ![]() границі квадрата (3.57) неодмінно перетне
криву
границі квадрата (3.57) неодмінно перетне
криву ![]() , якщо тільки
, якщо тільки ![]() не перевершує
деякого додатного числа
не перевершує
деякого додатного числа ![]() . З неперервності
функції
. З неперервності
функції ![]() маємо, що серед її значень на границі
квадрата можна знайти найбільше й найменше значення. Нехай
маємо, що серед її значень на границі
квадрата можна знайти найбільше й найменше значення. Нехай ![]() - найменше значення функції на границі
квадрата, тоді
- найменше значення функції на границі
квадрата, тоді ![]() .
.
Виберемо значення параметра ![]() таким, щоб
таким, щоб ![]() . На кривій
. На кривій ![]() функція
функція
![]() неперервна, тому на ній вона приймає всі
значення, що лежать між
неперервна, тому на ній вона приймає всі
значення, що лежать між ![]() й
й ![]() . Отже, у деякій точці
. Отже, у деякій точці ![]() кривої
кривої ![]() ця
функція прикмет і значення рівне
ця
функція прикмет і значення рівне ![]() . Але звідси маємо, що в
точці
. Але звідси маємо, що в
точці ![]() крива
крива ![]() перетинає
криву
перетинає
криву ![]() . Аналогічно доводиться ця властивість для
функції
. Аналогічно доводиться ця властивість для
функції ![]() .
.
Наслідок 1. Якщо ![]() , то поверхня
, то поверхня ![]() розташована
усередині поверхні
розташована
усередині поверхні ![]() , причому обидві ці поверхні не
мають загальних точок.
, причому обидві ці поверхні не
мають загальних точок.
Ознака 2. Якщо
точка, що ![]() зображує, переміщається убік зростання
обумовлено-додатної функції
зображує, переміщається убік зростання
обумовлено-додатної функції ![]() , то фазова траєкторія
цієї точки перетинає поверхню
, то фазова траєкторія
цієї точки перетинає поверхню ![]() зсередини назовні, а
при русі убік убування функції
зсередини назовні, а
при русі убік убування функції ![]() – зовні усередину (для
обумовлено-від’ємної функції
– зовні усередину (для
обумовлено-від’ємної функції ![]() – навпаки).
– навпаки).
Розглянуті властивості виконуються лише в досить малій околиці точки рівноваги (початку координат). Візьмемо на поверхні (3.62) довільну точку М и обчислимо в ній градієнт функції V:
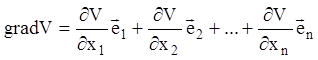 (3.63)
(3.63)
де ![]() -
орти осей
-
орти осей ![]() . Вектор
. Вектор ![]() спрямований
по нормалі до поверхні (3.62) у точці
спрямований
по нормалі до поверхні (3.62) у точці ![]() убік
зростання функції
убік
зростання функції ![]() , тобто зсередини поверхні
назовні у випадку безперечно додатної функції й зовні усередину цієї поверхні у
випадку обумовлено-від’ємної функції.
, тобто зсередини поверхні
назовні у випадку безперечно додатної функції й зовні усередину цієї поверхні у
випадку обумовлено-від’ємної функції.
Введемо в розгляд швидкість ![]() точки, що
точки, що ![]() зображує. З рівнянь збуреного руху (3.56)
маємо, що функції
зображує. З рівнянь збуреного руху (3.56)
маємо, що функції ![]() є проекціями вектора швидкості
є проекціями вектора швидкості ![]() на відповідні осі
на відповідні осі ![]() .
Але тоді формулу (3.60), з огляду на (3.63), можна представити у вигляді
.
Але тоді формулу (3.60), з огляду на (3.63), можна представити у вигляді
![]() (3.64)
(3.64)
Похідна ![]() дає можливість простежити за
рухом точки, що
дає можливість простежити за
рухом точки, що ![]() зображує .
зображує .
Нехай у цей момент ![]() точка
точка ![]() займає певне положення на фазовій площині.
Візьмемо довільну обумовлено-додатною функцію
займає певне положення на фазовій площині.
Візьмемо довільну обумовлено-додатною функцію ![]() й
побудуємо поверхню
й
побудуємо поверхню ![]() , що проходить через точку
, що проходить через точку ![]() .
.
а) якщо в розглянутому положенні точки ![]()
![]() , то функція
, то функція ![]() убуває,
а це значить, що точка, що
убуває,
а це значить, що точка, що ![]() зображує, переходить
зовні усередину
зображує, переходить
зовні усередину ![]() поверхні (див. наслідок 2)
поверхні (див. наслідок 2)
б) якщо ![]() , т з (3.64) маємо, що кут між
векторами
, т з (3.64) маємо, що кут між
векторами ![]() й
й ![]() прямій,
тобто, що фазова траєкторія в розглянутому положенні точки
прямій,
тобто, що фазова траєкторія в розглянутому положенні точки ![]() торкається поверхні
торкається поверхні ![]() .
.
в) якщо ![]() , те функція V зростає, а це
значить, що точка, що зображує, переходить зсередини назовні поверхні V=C.
, те функція V зростає, а це
значить, що точка, що зображує, переходить зсередини назовні поверхні V=C.
Теорема1. Якщо
диференціальні рівняння збуреного руху такі, що можна знайти знаковизнечену
функцію ![]() , похідна
, похідна ![]() якої в
силу цих рівнянь була б знакопостійною функцією протилежного зі
якої в
силу цих рівнянь була б знакопостійною функцією протилежного зі ![]() знака або тотожно дорівнює нулю, то
незбурений рух стійкий.
знака або тотожно дорівнює нулю, то
незбурений рух стійкий.
Доведення. Для гарної
наочності результатів доказ проведемо для ![]() .
.
Виберемо довільне ![]() й побудуємо квадрат
(3.57). Потім усередині цього квадрата побудуємо криву
й побудуємо квадрат
(3.57). Потім усередині цього квадрата побудуємо криву ![]() =С.
Це завжди можна зробити, тому що функція V неперервна й дорівнює нулю на
початку координат. Побудуємо далі квадрат
=С.
Це завжди можна зробити, тому що функція V неперервна й дорівнює нулю на
початку координат. Побудуємо далі квадрат
![]() ,
, ![]() (3.65)
(3.65)
так, щоб він лежав усередині
кривій ![]() . Для визначеності покладемо, що
. Для визначеності покладемо, що ![]() – обумовлено-додатня функція. Тоді в силу
теореми
– обумовлено-додатня функція. Тоді в силу
теореми ![]() й
й 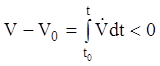 , де
, де ![]() - значення функції
- значення функції ![]() при
при
![]() . Тоді
. Тоді ![]() . З
останньої нерівності й результатів попереднього параграфа маємо, що при
. З
останньої нерівності й результатів попереднього параграфа маємо, що при ![]() точка
точка ![]() ,
почавши рух з будь-якої
,
почавши рух з будь-якої ![]() точки квадрата (3.65),
за увесь час руху не вийде за межі квадрата (3.57), звідки й витікає стійкість
незбуреного руху.
точки квадрата (3.65),
за увесь час руху не вийде за межі квадрата (3.57), звідки й витікає стійкість
незбуреного руху.
Проведемо доказ у загальному випадку.
Нехай для визначеності для системи (3.56) існує знаковизначена додатна
функція Ляпунова ![]() . Це не обмежує спільності
міркувань, тому що множенням на (-1) знакододатні функції звертаються в
знаковід’ємні й навпаки.
. Це не обмежує спільності
міркувань, тому що множенням на (-1) знакододатні функції звертаються в
знаковід’ємні й навпаки.
Позначимо через ![]()
![]() -мірну
кулю радіуса
-мірну
кулю радіуса ![]() фазового простору із центром на початку
координат, а через
фазового простору із центром на початку
координат, а через ![]() - поверхню кулі. Нехай
- поверхню кулі. Нехай ![]() на поверхні кулі при
на поверхні кулі при ![]() . Підберемо таке
. Підберемо таке ![]()
![]() , щоб для будь-якої точки кулі
, щоб для будь-якої точки кулі ![]() виконувалася нерівність
виконувалася нерівність ![]() при
при ![]() .
Виберемо якусь точку
.
Виберемо якусь точку ![]() і розглянемо траєкторію
і розглянемо траєкторію ![]() , що починається в точці
, що починається в точці ![]() . Припустимо, що ця траєкторія при
. Припустимо, що ця траєкторія при ![]() виходить за межі сфери
виходить за межі сфери ![]() в деякій точці
в деякій точці ![]() ,
, ![]() і покажемо, що наше допущення суперечливо.
і покажемо, що наше допущення суперечливо.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.