Ряди з позитивними членами. Критерій збіжності. Теореми порівняння. Ознаки Даламбера і Коші. Інтегральна ознака Коші

Лекція 2

План.

1.  Ряди з позитивними членами. Критерій збіжності. Теореми порівняння.

2.  Ознаки Даламбера і Коші.

3.  Інтегральна ознака Коші.

1. Ряди з позитивними членами. Критерій збіжності. Теореми порівняння.

Теореми порівняння

Теорема 1. Дано два ряди з позитивними членами

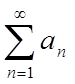                                                  (1)

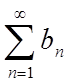і                                                                                                              (2)

причому

                                                (3)

і ряд (2) збігається, то збігається і ряд (1).

Доказ.

Тому що за умовою ряд (2) збігається, то існує 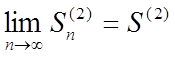, де .

Складемо

,

– n-я часткова сума ряду (1).

Відповідно до нерівності (3) ; тому що послідовність часткових сум  є обмеженою, 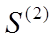, то і послідовність  n-х часткових сум ряду (1) (монотонно зростаюча) також є обмеженою, і, отже, вона має кінцеву межу. По визначенню 3 це означає, що ряд (1) збігається.

Наприклад: 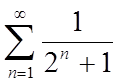 (1) і 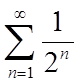 (2) – дані два ряди. Причому,  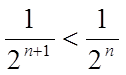(3).

Ряд (2) – сума убутної геометричної прогресії, тобто він збігається. Отже, по теоремі 1 збігається і ряд (1).

Теорема 2. Дано два ряди з позитивними членами

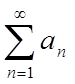                                                  (1)

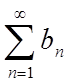і                                                                                                              (2)

причому виконується нерівність

                                                 (4)

і ряд (2) розбігається, то розбігається і ряд (1).

Доказ.

З (4) випливає, що , тому що члени ряду (2) позитивні, то його часткова сума зростає при зростанні n, а тому що він розбігається, то .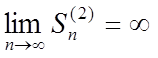

Тоді в силу (4)

,

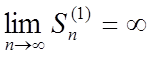тобто ряд (1) розбігається.

Зауваження 1. На практиці зручно використовувати так звану граничну ознаку порівняння.

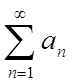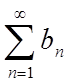Дано два ряди з позитивними членами  (1);  (2).

Якщо 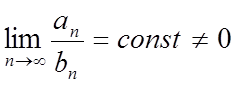 і відомо, що один з рядів збігається (розбігається), то тоді другий з цих рядів збігається (розбігається).

Зауваження 2. Теореми (1) і (2) справедливі й у тому випадку, якщо нерівності (3) і (4) починають виконуватися лише для , а не для всіх

2. Ознаки Даламбера і Коші.

Ознака Даламбера

Якщо в ряді з позитивними членами 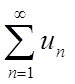 (1) відношення  члена до n-му при  має кінцеву межу l, тобто 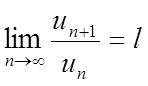, то при  ряд збігається, при  – розбігається, при  відповіді на питання про збіжність або розбіжність ряду теорема не дає.

Доказ.

1. Нехай .

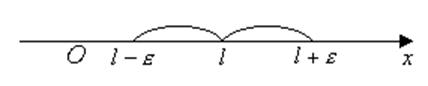З визначення межі випливає, що має місце нерівність

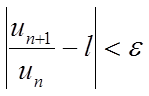, при ,

де ε як завгодно мале число.

Тоді розглянемо праву частину нерівності

,

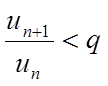відкіля

Просумуємо ліві і праві частини отриманих нерівностей.

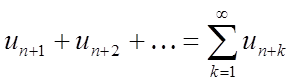 – ліві частини,

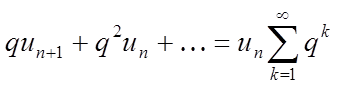 – праві частини, що убуває геометрична прогресія.

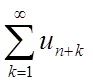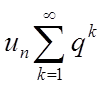Порівнюючи два ряди  і  за умови виконання нерівності  по теоремі порівняння укладаємо, що ряд 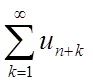 – збігається.

По 3-й властивості рядів, що збігається, при додатку до 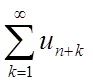 ряду кінцевого числа  доданків одержимо ряд що збігається. Отже, ряд (1) збігається.

2. Нехай , тоді 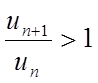 (з визначення межі) при , тобто  для всіх , і тому загальний член ряду не прагне до нуля. По наслідку з необхідної ознаки ряд розбігається.

Зауваження. Ознаку Даламбера зручно застосовувати, якщо загальний член ряду містить факторіали, показову функцію.

Наприклад: дослідити збіжність ряду

;                    ;         

,

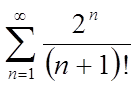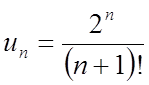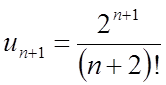
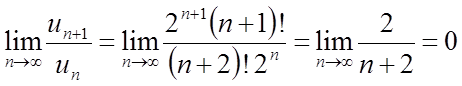виходить , отже, ряд збігається.

Радикальна ознака Коші

Теорема. Дано ряд з позитивними членами 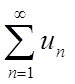 й існує кінцева межа 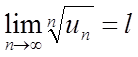. Якщо  – ряд збігається, якщо  – ряд розбігається, при  питання про збіжність ряду ознака не вирішує.

Доказ.

З визначення межі випливає

,                   ,

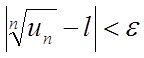ε – як завгодно мале позитивне число.

.

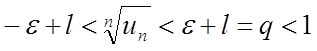Розглянемо праву частину нерівності

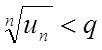      або    .

Просумуємо ліві і праві частини отриманої нерівності

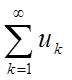                                                   (7)

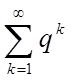                                                   (8)

Ряд (8) збігається, тому що його члени утворять убутну геометричну прогресію. Члени ряду (7) починаючи з  – менше членів ряду (8). Отже, ряд (7) збігається.

2. Нехай . Тоді починаючи з деякого номера n = N

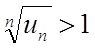       або    .

Ряд (7) розбігається, тому що його загальний член не прагне до нуля.

Наприклад: дослідити збіжність ряду .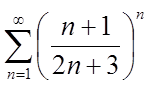

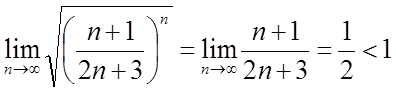 – ряд розбігається.

3. Інтегральна ознака Коші

Теорема. Нехай даний ряд 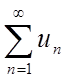 (1) з позитивними членами, причому

1)  Члени ряду зростають.

2)  Нехай  така безперервна незростаюча функція, що , ,…,,…

Тоді, якщо невласний інтеграл 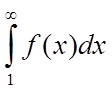 збігається, то збігається, і ряд (1), якщо зазначений інтеграл розбігається, то розбігається і ряд (1).

Доказ.

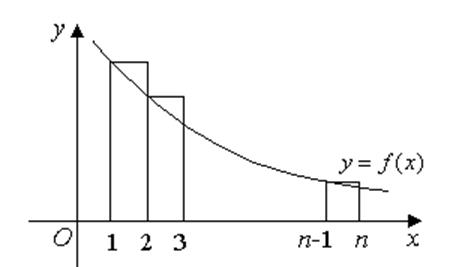Зобразимо члени ряду геометрично, відкладаючи по осі абсцис номера членів ряду, а по осі ординат – значення членів ряду . Побудуємо на кресленні графік функції .

Площа східчастої фігури

.

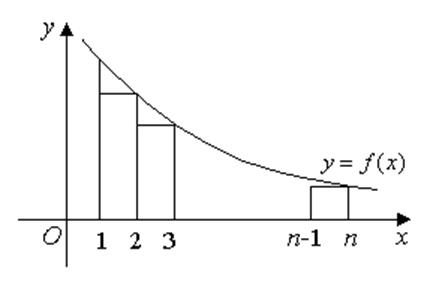
Площа східчастої фігури

.

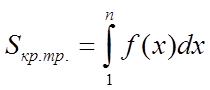; з побудови випливає

.

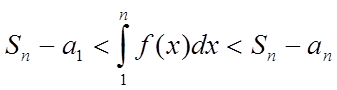1. Нехай невласний інтеграл збігається

.

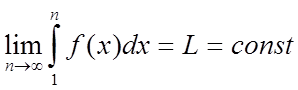Розглянемо ліву частину нерівності (3). Тому що 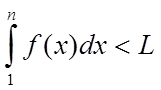, те  (монотонно зростаюча й обмежена зверху), отже, послідовність n часткових сум ряду має кінцеву межу і ряд (1) збігається.

2. Нехай невласний інтеграл розбігається, тоді з правої частини нерівності (3) при  одержуємо, що послідовність  необмежено зростає при , тобто ряд (1) розбігається.

Наприклад: досліджувати збіжність ряду 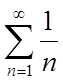 (гармонійний ряд).

Загальний член 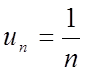 задовольняє умовам інтегральної ознаки. Розглянемо інтеграл

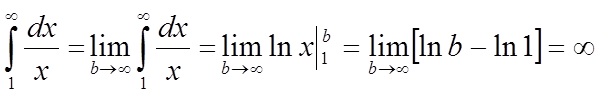
Виходить, ряд розбігається.