



Лекція 3
План.
1. Поняття комплексного числа. Основна теорема алгебри.
2. Багаточлени і їхні корені, розкладання багаточленів на множники.
3. Раціональні дроби, їхнє розкладання на найпростіші.
1. Поняття комплексного числа. Основна теорема алгебри.
До введення комплексного числа
змусила вимога, щоб усякому квадратному рівнянню й навіть усякому алгебраїчному
рівнянню можна було приписувати відоме рішення. Якщо, наприклад, хочуть, щоб
рівняння ![]() мало корені, то доводиться ввести нові
символи + i та –i у властивості коренів цього рівняння (й цим
одночасно досягається, як доводиться в алгебрі, те що усі алгебраїчні рівняння
алгебри вирішуються).
мало корені, то доводиться ввести нові
символи + i та –i у властивості коренів цього рівняння (й цим
одночасно досягається, як доводиться в алгебрі, те що усі алгебраїчні рівняння
алгебри вирішуються).
Той факт, що будь-яке алгебраїчне рівняння має дійсні або комплексні корені, складає склад так званої “основної теореми ” алгебри.
Основна теорема алгебри:
Будь-який багаточлен
степеню ![]() має хоча б один комплексний (речовий або
уявний) нуль, тобто корінь.
має хоча б один комплексний (речовий або
уявний) нуль, тобто корінь.
Якщо а та b – звичайні дійсні числа, то комплексне число с = а + ib означає ні що інше, як пару чисел (а; b), причому дії над подібними парами робляться просто за наступним правилом.
Комплексні числа а + ib (у склад яких входить у якості приватного випадку при b=0 також й дійсні числа) складають, помножують, ділять, розглядаючи позначку i як невизначену величину, а потім спрощують усі вираження, що містять i у степенях вище першого, користуючись співвідношенням i2 = – 1, так що i зостається тільки в першому степені й знову отримаємо вираження у вигляді а + ib.
2. Багаточлени і їхні корені, розкладання багаточленів на множники
Функція виду ![]() , де n – натуральне число, ai
(i = 0, 1, …, n) – постійні коефіцієнти, називається багаточленом (або
цілою раціональною функцією).
, де n – натуральне число, ai
(i = 0, 1, …, n) – постійні коефіцієнти, називається багаточленом (або
цілою раціональною функцією).
Ціла раціональна функція(багаточлен) інтегрується безпосередньо.
Теорема. Усякий багаточлен з
дійсними коефіцієнтами розкладається на лінійні і квадратні множники з дійсними
коефіцієнтами, тобто багаточлен ![]() можна представити у
виді:
можна представити у
виді:
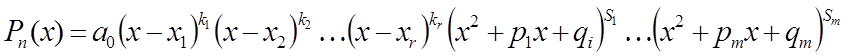
причому всі квадратні тричлени не мають речовинних коренів.
3. Раціональні дроби, їхнє розкладання на найпростіші
Нехай ![]() і
і ![]() –
багаточлени. Функція виду
–
багаточлени. Функція виду 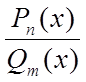 називається
раціональним дробом. Якщо ступінь чисельника нижче ступеня знаменника, тобто n
< m, то раціональний дріб називається правильним; якщо n ≥ m, те
дріб – неправильним. Наприклад,
називається
раціональним дробом. Якщо ступінь чисельника нижче ступеня знаменника, тобто n
< m, то раціональний дріб називається правильним; якщо n ≥ m, те
дріб – неправильним. Наприклад, 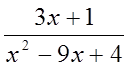 – правильний дріб, а
– правильний дріб, а 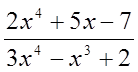 і
і 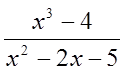 –
неправильні дроби.
–
неправильні дроби.
Найпростішими дробами називаються дроби виду:
I. 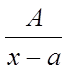 .
.
II. 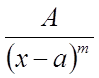 , де m
– ціле число, причому m ≥ 2.
, де m
– ціле число, причому m ≥ 2.
III. 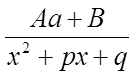 , де
, де 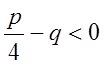 , тобто знаменник не має дійсних коренів.
, тобто знаменник не має дійсних коренів.
IV. 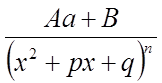 , де n
– ціле число, причому n ≥ 2, а знаменник не має дійсних коренів.
, де n
– ціле число, причому n ≥ 2, а знаменник не має дійсних коренів.
В усіх чотирьох випадках А, В, p, q, a – дійсні числа.
Перед
інтегруванням раціонального дробу 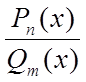 треба зробити наступні
перетворення й обчислення:
треба зробити наступні
перетворення й обчислення:
1) якщо
дріб 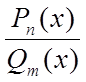 неправильний, то виділяємо цілую частину,
тобто поділяємо чисельник на знаменник і записуємо у вигляді:
неправильний, то виділяємо цілую частину,
тобто поділяємо чисельник на знаменник і записуємо у вигляді:
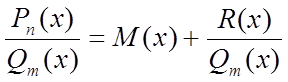 ,
,
де М(х) – багаточлен, а 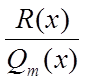 – правильний раціональний дріб;
– правильний раціональний дріб;
2) розкладемо знаменник на множники (лінійний і квадратні);
3)
правильний
раціональний дріб 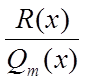 розкладемо на найпростіші дроби:
розкладемо на найпростіші дроби:
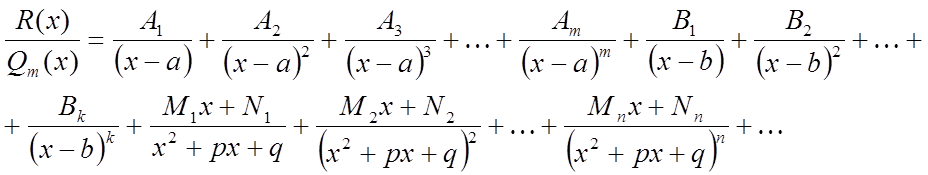
Тут коефіцієнти ![]() – невизначені коефіцієнти, поки вони
невідомі;
– невизначені коефіцієнти, поки вони
невідомі;
4)
щоб
визначити ці коефіцієнти, останню рівність приводимо до загального знаменника,
відкидаємо знаменник і дорівнюємо коефіцієнти при однакових ступенях х у
лівій і правій частинах отриманої рівності. Одержимо систему лінійних рівнянь,
вирішивши яку, знайдемо коефіцієнти ![]()
Для знаходження
коефіцієнтів можна використовувати наступне зауваження: тому що отримана
рівність виконується при всіх значеннях х, то вона буде виконуватися і
при відомих значеннях х, рівних дійсним кореням багаточлена ![]() , або х можна додати будь-які
приватні значення. Описаний метод називається методом невизначених
коефіцієнтів.
, або х можна додати будь-які
приватні значення. Описаний метод називається методом невизначених
коефіцієнтів.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.