Определители, их свойства, методы вычисления

П.з №2.

Определители ,их свойства, методы вычисления.

Матрицей размера   называется прямоугольная таблица чисел или функций, имеющая m строк и n столбцов.

A,B,C,…   

                 

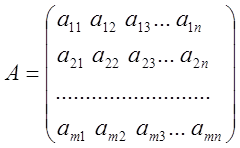
a_ij , i- строка ,j-столбец

Обозначение : A,B,C,…

При m=n матрица становится квадратной и в этом случае говорят о матрице порядка n.

            С понятием матрицы тесно связано понятие определителя. Понятие определителя возникло в связи с проблемами решения системы n линейных алгебраических уравнений с n неизвестными.

Определителем n-го порядка называется число ,которое ставится в соответствие кв.матрице порядка n и обозначается: | A | , det A; D, det (a_ij)

Определитель 2-го порядка- это число

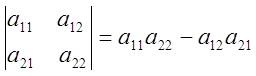
ПРИМЕРЫ.

 

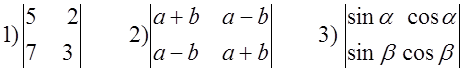
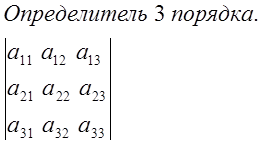
а) правило  .

б) по правилу Саррюса (модификация пр. ).

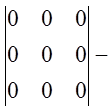
а)      б)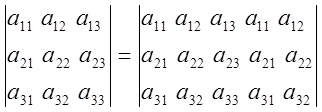    

Примеры:

4)

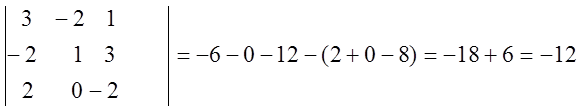
5) 

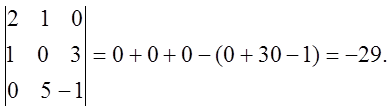
Свойства определителей:

1.  Определитель не изменится при замене всех его строк  соответствующими столбцами.

2.  При перестановке двух столбцов (строк) определитель меняет знак .

3.  Определитель с двумя одинаковыми столбцами (строками)=0.

4.  Множитель, общий для элементов некоторого столбца (строки),можно выносить за знак определителя.

5.  D =0,если все элементы некоторого столбца (строки) =0.

6.  D с двумя пропорциональными столбцами(строками)=0

7.      a₁₁’+a₁₁”       a₁₂  a₁₃            a₁₁’  a₁₂  a₁₃           a₁₁”  a₁₂  a₁₃

    a₂₁’+a₂₂”      a₂₂   a₂₃    =     a₂₁’  a₂₂  a₂₃     +    a₂₁”  a₂₂  a₂₃  

    a₃₁’+a₃₂”      a₃₂   a₃₃           a₃₁’  a₃₂  a₃₃           a₃₁”  a₃₂  a₃₃   

8.  D не изменится ,если к элементам некоторого столбца (строки) прибавить соответственные  элементы другого столбца (строки),предварительно умножив их на одно и тоже число.

9.  D равен сумме прроизведений элементов какого-либо столбца (строки)на их алгебраические дополнения.

          D=a₁₁ A₁₁ + a₁₂ A₁₂ + a₁₃ A₁₃ .

Минором  некоторого элемента называется определитель, получаемый из данного путем вычеркиваниия строки и столбца, на пересечении которых расположен этот элемент.

Алгебраическим дополнением  элемента Аij  называется минор этого элемента, взятый со своим знаком, если (i+j) – четная величина,и с противоположным,если (i+j) –нечетная.

Aij=(-1) ^i+j   Mij

ПРИМЕРЫ:

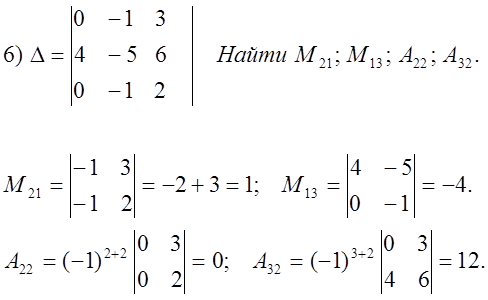
7.Пользуясь свойством 9 , вычислить  D.

                       

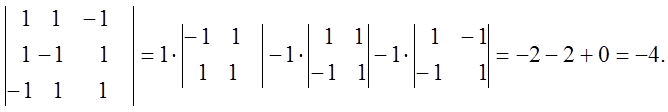
8. Пользуясь свойством 9 , вычислить  D.

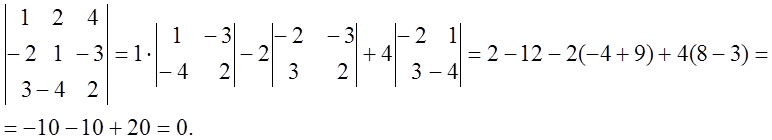
9. Вычислить , пользуясь свойствами:

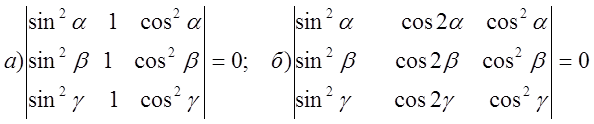
10. Вычислить определитель , приведя его к треугольному виду:

 

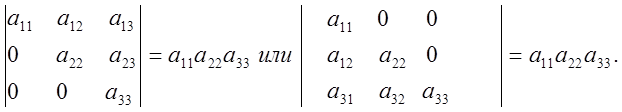
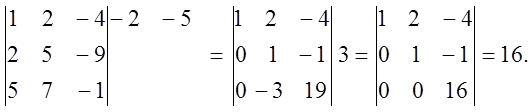
   Преобразование строки (столбца)

     =  

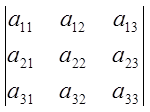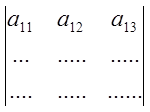
                    начало стрелки указывает на строку, которая не изменяется, конец стрелки указывает на появление новой строки.

  связан с концом стрелки.

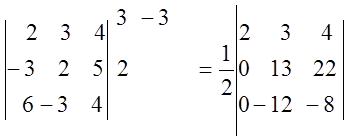11.  =×2×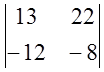 = -104+264=160

12. 

Пp.з.  № 3 .   

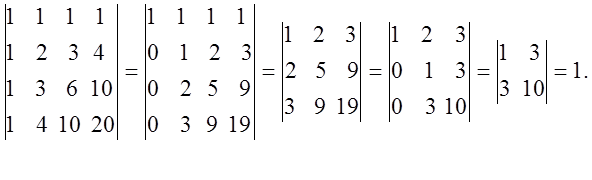
Решение систем линейных алгебрарических уравнений (СЛАУ) с помощью определителей.  Формулы Крамера.

СЛНАУ                                                 СЛОАУ

a₁₁x₁+a₁₂x₂+…+a_1nx_n=b₁                    a₁₁x₁+…+a_1nx_n=0

……………………………….  (1)           …………………..       (2)

a_m1x₁+a_m2x₂+…+a_mnx_n=b_m                 a_m1x₁+…+a_mnx_n=0

 Система называется неоднородной ,если среди свободных членов имеются отличные от 0. (1)

Если все свободные члены =0, то однородная система.

Система, имеющая хотя одно решение называется совместной, а не имеющая ни одного решения – несовместной.

Совместная система, и меющая единственное решение ,называется определенной.

Совместная система, имеющая более одного решения, называется неопределенной.

Если m=n, то систему то  систему можно решить с помощью определителей.

            Все возможные случаи рассмотрим на примере системы 3-х уравнений с3 неизвестными.

   Аналогично ,при n>3.

   Г. Крамер (1704-1752) –швейцарский математик.

D	D1	D2	D3	Вывод
¹0				Система определенная . Единственное решение формулы Крамера: X1=; X2=; X3=
=0	¹0или	¹0или	¹0	Система  несовместна Нет решений.
=0	=0	=0	=0	Система неопределенная, решений бесчисленное множество.

 

1.        3x₁+ x₂ =7             3    1                           7     1                           3    7              .                        ∆=                =5       ∆₁  =                   =20    ∆₂=                   =-25

     4x₁+3x₂=1              4    3                           1     3                           4    1