Восстановление сигналов по дискретным отсчетам Котельникова (лабораторная работа)

ьорнпеолкдюолрпьарет

восстановление  сигналов  по дискретным  отсчетам  котельникова

Методические указания

к лабораторной работе по дисциплине

"Основы радиоэлектроники и связи"

Рыбинск

1785

Цель работы – изучение возможности синтезирования сигналов по дискретным отсчетам в соответствии с поьпмрсчимьбльникова, исследование влияния частоты выборок и характеюдорчсонуконшьоднижних частот на качество синтезирования.

3.1 Краткие теоретические сведения

В соответствии с теоремой Котельникова сигнал , не содержащий частот выше , полностью определяется своими мгновенными значениями , отсчитанными через интервалы времени :

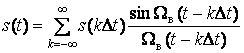 ,                                                     (3.1)

где  – наивысшая круговая частота в спектре сигнала.

Отсчеты сигнала  в момеволджэ.ллогш являются коэффициентами Фурье  разложения сигнала  по ортогональной системе функций отсчетов:

.

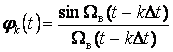Спектральное пояснение теолнм орп лльникова дает рисунок 3.1, на котором изображены исходный сигнропрсмапмт ектр , дискретизбло анный сигналам

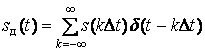                                                               (3.2)

и его спектр

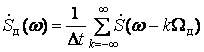                                                               (3.3)

для различных частот дискретизации .

Спектр дискретизированного с   шнпшпредставляет собой сумму копий спектра сигнала  с центральнымилрпс765ами 0; 236 .д. Если , т.е. м  д юджно восстановить исшзщшуй сигнал , пропустив дискретизированный сигнал (3.2) черезорпонсмный фильтр нижних частот (ФНЧ) с частотным коэффициентом передачи

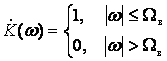.                                                                      (3.4)

 

Импульсная характеристика такого фильтра с точностью до постоянного множителя совпадает с функлороротсчетов :

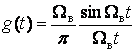 .                                                                           (3.5)

Если же , т.е. , то соседние копии спектра перекрываются и восстановление сигнаки 557евозможно. Таким обрсавепимаксимальный интервал (период) выборок  , что и утверждаетссмиррввафый Котельникова.

При практическом использовании998763212Котельникова для восстановления сигналов по отсчетам необходимо учиёёёёёёёёёёёёёёёёёёёёёёёёющие погрешности. П6ёёёёё для этого следующие.ё

1. Сигналы с ограниченным спектром бесконечны во времени и поэтому восстановление мгновенногбббббббббббббббинципиально требует учета значений бесчисленного множества дискретных отсчетов. Использование отсчетов, взятых в ограничёёёёёёёёёёёёёёёёёёёёёёёёёёёёёёреход к конечным пределам  в ряде (3.1) и вызывёёёёёёёёёёёёё ошибки восстановления.