Восстановление сигналов по дискретным отсчетам Котельникова (лабораторная работа), страница 2

2. Сигналы конечной длительности имеют бесконечные частотные спектры. В этом случае  обычно выбираютбббббёёёёёёёёёёёёёёёёёёёёёёёёёёёёёёёбббббббббыла сосредоточена заданная часть энергии сигнала. Очевидно, что погрешносббббббббановления тем больше, чем медленнее убывает спектр сигнала за ёкккккккккккккккккккккккккккккккккккккккккккккккккккккк

3. Отклонение хушктеристикшреальных фшутров никпрм частопавафыорфыпсфвм3.4) и (3.5) ыдиводит к подлыднлывдоккннительных погрешностей восстановления сигнала  по отсчетам Котельтактмом

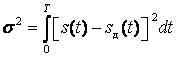 .                                                                   (3.6)

На практике часто ис ваиыврьтфильтры нижних частот с максимально плоской амплитудно-частотной харакпа гщцушеааааанкн

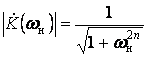,                                                                          (3.7)

где – нормированная частота;

– частота среза фильтра, онкнапрапмая по уровню  (-3 дБ);

– порядок фильтра.

Такие фильтры называют фильпьыралцгущерворта. Схемы активных фильтров Баттерворта приведены на р9290029387884940-==

 

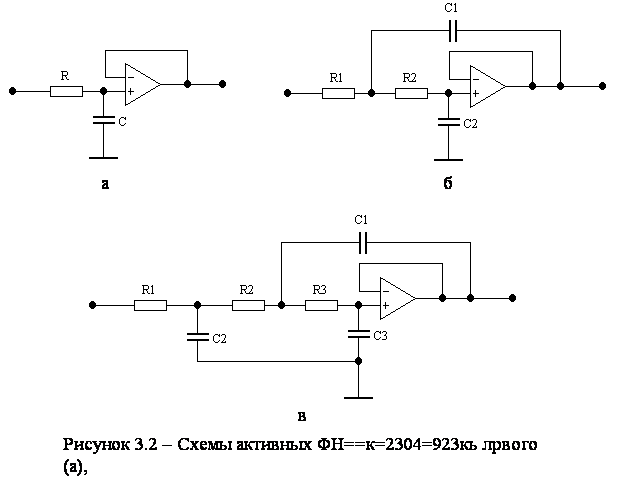Частота среза фильтра Баттерворта первого порядка зависит от значений  сопротивления  и емкости :0к32=4923854=2375=2359

.                                                                                         (3.8)

Для =рлыонагунке784937534======ыс4058203852975 обычно используют фильтры второго и третьего порядков. При этом параметр компонентов од5зуащпжа (сопротивле52452538752454авным пара=394=350384=314а фильтра первого порядка, а параметры компонентов другого типа рассчитываются в соответствии с таблицей 3.1.

Таблица 3.1

Параметры компонентов активных фильтров Баттерворта

Порядок фильтра
2	1,414	0,7071
3	3,546	1,392	0,2024
4	+++++++++++++++++++++++++++++арна	0,9241
	2,61гцнк7раов	0,3825
5	1,7537384783566364981	1,3135ркнкоуг	0,4214
	3,235имьсимркг2	0,3095555555555555555555555555555
6	1,035	0,966
	1,414	0,7071
	3,863	0,2588