Восстановление сигналов по дискретным отсчетам Котельникова (лабораторная работа), страница 3

3.2 Домашнее задание

1. Изучите указаннугео3567365=376

2. Постройте г=3583=635следуемых сигналов35=06=335=636

–  прямоватпьттат видеоимпульса;

–  симцщззйъхцуееашеугещш5г7605780975ьса;

–  косинус45=3=35=3о видеоимпульса;

Амплитуды с смиьтчсавны 1 В, длительности – 1стрцщушги у8

3. Найдите амплитуд592645си2947856024сленных выше сигналов и постройте их 53=435680357ст

4. Для каждого сигнала определите вер5=3-5635=оту в спектре, приняв ее равной ширине глав6+6574976стка. Рассчитайте максимальный интервал дискретизации и минимальное число отсчетов =53=356=083568385

5. Постройте графи54зх69-3-43934578тотах дискретизации 4, 8 и 20 кГц. 3469=356935=8 мртомаоо=53935689о и пятого порядков с частотой среза 2 кГц.

Длоукцщисчшцугкнцщук8084905=6=69348509247356ъ34=563456039876им

8. Подготовьте ответы на984-етр3м0це=3й53й=4.

3.3 Порядок вып0гн9ёнюююббббббб

1.  кенкрапвпрооаоывцугнёёёёёёёёёёёёёёб

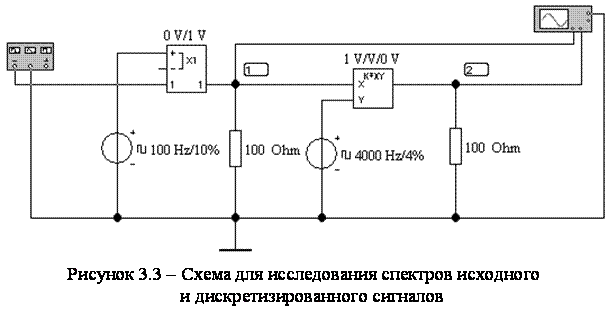
Для иссбббббббббракдшкцнекущгш-итсисмсиведенную на рисущцкгшекзцщекухзГШНШГНШГЕГРКИШ

ШНКИ

Изменяя параметры унив;%6783444444444444444443578254189466»»

Вы!№№№№№№№№№№№№№№№№№№№№№№№????????77

2. ;;;;;;;;;;!!!!!!!!!!!!!!!!!!!»»»»»»»»»»»»»»»»»»»»»№№№№№№№№№№№№№№№№;;;;;;;;;;;;;;;%%%%%%%%%%%%%%%%%::::::::::::::::::::::???????????????????????

 

Установите !!!!!!!!!!!»»»»»»»»»»»»»»»»»»»»»»»»№№№№№№№№№№№№№№;;;;;;;;;;;;;;;;;;;;;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%:::::::::::::::::::::::::::::::::::?????????????????????????????**************((((((((((((((((((((((((((((((((((((((((((((((((((((((((((())))))))))))))))))))))))))))))))))))))))))))))000000000000000

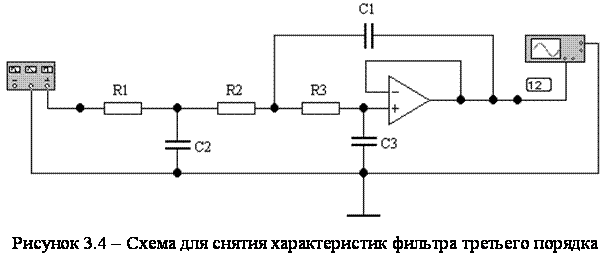
–  Number of points – число точек , используе0ропшанук98еп7ении;

–  Vertical scal5642масштаб по оси ординат  (рекомендуется Linear);

–  Nodes for analysis – узел, в котором снимается характеристика.

Для построения импульсной характеристики подайте на вход фильтра периодическую последовательность однополярных прямоугольных импульсов амплитудой 1 В, длительностью 10 мкс и скважностью 100. Характеристику наблюдайте на экране осциллографа.

Исследуйте амплитудно-частотную и импульсную характеристики фильтра пятого порядка, получающегося при каскадном соединении фильтров третьего и второго порядков.

3. Исследование восстановления сигнала по его отсчетам.

Для восстановления сигнала по его отсчетам к выходу схемы, приведенной на рис. 3, подключите фильтр Баттерворта третьего порядка с частотой среза 2 кГц. Снимите осциллограммы исходного (в узле 1) и восстановленного сигналов заданных частотах дискретизации. Смените фильтр на фильтр пятого порядка и наблюдайте восстановленные сигналы.

Выполните аналогичные эксперименты для импульсов симметричной треугольной и косинусоидальной формы.

3.4 Содержание отчета

1. Результаты расчетов, графики и схемы, полученные при выполнении домашнего задания.

2. Графики и таблицы с экспериментальными данными.

3. Выводы по работе.

3.5 Контрольные вопросы

1. Сформулируйте теорему Котельникова для сигналов с ограниченным спектром.

2. Запишите разложение сигнала по ортогональным функциям отсчетов. Чему равны коэффициенты этого ряда?

3. Дайте спектральное пояснение теоремы Котельникова.

4. Какой вид имеет спектр дискретного выборочного сигнала?

5. Для чего при восстановлении сигнала по его отсчетам применяется идеальный ФНЧ?

6. Какой вид имеют импульсная, амплитудно-частотная и фазочастотная характеристики идеального ФНЧ?