Наблюдаемость в линейных системах управления: Практическое занятие № 5

Практическое занятие  5.

Тема: Наблюдаемость в линейных системах

управления.

Цель занятия : ознакомление с методикой исследования наблюдаемости систем управления, вопросами двойственности управляемости и наблюдаемости. Выделение наблюдаемых фазовых координат с помощью построения канонической формы системы управления.

Пусть система управления описывается следующими уравнениями:

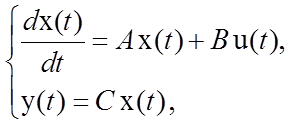                               (5.1)

где , , – непрерывные матрицы порядка , ,  соответственно;  – -вектор выходных (измеряемых) координат системы управления.

В случае, если система (5.1) стационарна и , то матрица наблюдаемости  примет вид

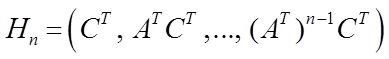                               (5.2)

или

,

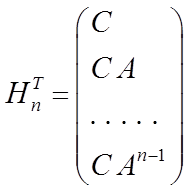а формула (5.2) при :

.

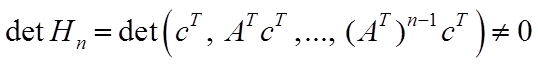Пример.

Пусть стационарная линейная система управления описывается следующими дифференциальными уравнениями в нормальной форме:

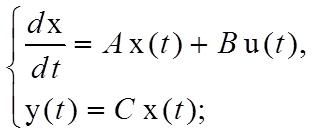
где       ;      ;      .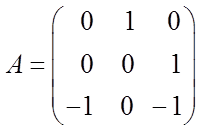

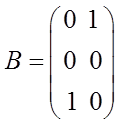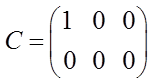Исследовать управляемость и наблюдаемость системы.

Решение.

Построим матрицу управляемости исходной системы

,

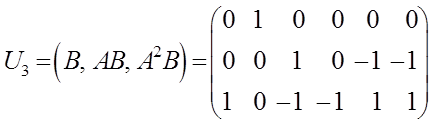где    ;    .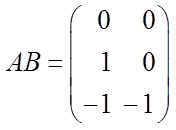 

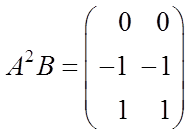Матрица  содержит линейно независимые столбцы, например, 1-ый, 2-ой и 3-ий. Следовательно, 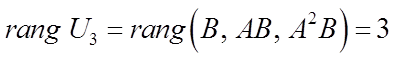 и система управляема.

Матрица наблюдаемости

,

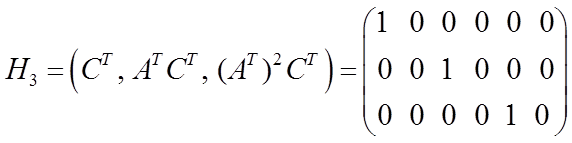где               ;    .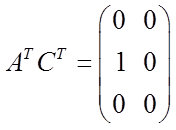 

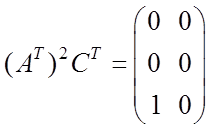В матрице  1-ый, 3-ой и 5-ый столбцы линейно независимые. Таким образом, 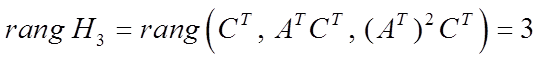 и система управления наблюдаема, т.е. по измеряемой фазовой координате 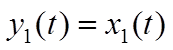 путем несложных преобразований можно восстановить ненаблюдаемые фазовые координаты  и .

Задачи.

1. Стационарная линейная система управления описывается следующими дифференциальными уравнениями в нормальной форме:

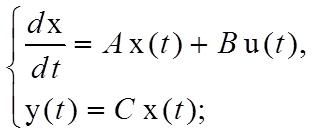
где       ;      ;      .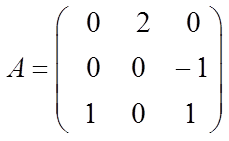

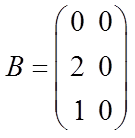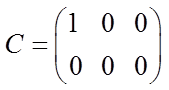Исследовать управляемость и наблюдаемость системы. Если система не наблюдаема, то определить ненаблюдаемые фазовые координаты.

2. Стационарная линейная система управления описывается следующими дифференциальными уравнениями в нормальной форме:

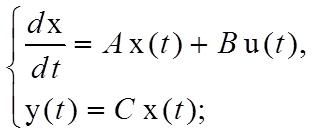
где       ;      ;      .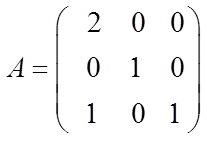

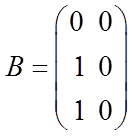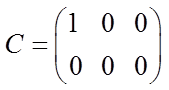Исследовать управляемость и наблюдаемость системы. Если система ненаблюдаема, то определить ненаблюдаемые фазовые координаты.

Список рекомендуемой литературы.

1.  Атанс М., Фалб П. Оптимальное управление. М., «Машиностроение», 1968.

2.  Беллман Р., Калаба Р. Динамическое программирование и современная теория управления. –М.: Наука, 1969.

3.  Болтянский В.Г. Математические методы оптимального управления. –М.: Наука, 1968.

4.  Брайсон А., Хо Ю-ши Прикладная теория оптимального управления. Оптимизация, оценка и управление. М.: Мир, 1972. –544 с.

5.  Нефедов Ю.М. Теория управления. Учеб. пос. –Луганск: Изд-во ВНУ им. В.Даля, 2003. – 228 с.