




Практическое занятие 6.
Тема:
Задача построения оптимального управления может быть сформулирована как вариационная задача. При этом кроме уравнений объекта управления должны быть заданы краевые условия и выбран критерий оптимальности. Кроме того, могут быть заданы ограничения на управление и фазовые координаты.
Пример 6.1.
Рассмотрим задачу об оптимальном управлении электроприводом, динамика которого описывается системой уравнений
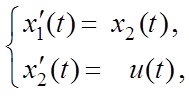 (6.1)
(6.1)
где
![]() – угол поворота вала электродвигателя и
– угол поворота вала электродвигателя и ![]() – скорость поворота.
– скорость поворота.
Необходимо определить оптимальный процесс перевода системы (6.1) из одной точки фазового пространства
![]() ,
, ![]() , (6.2)
, (6.2)
в другую заданную точку фазового пространства
![]() ,
, ![]() (6.3)
(6.3)
за
фиксированный отрезок времени ![]() , затрачивая при этом
минимум энергии управляющего сигнала, т.е. функционалом минимизации, является интеграл
, затрачивая при этом
минимум энергии управляющего сигнала, т.е. функционалом минимизации, является интеграл
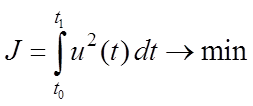 .
.
Для построения конкретных временных диаграмм
предположим, что ![]() ,
, ![]() .
.
Решение.
Для определения оптимального управления ![]() и оптимальной фазовой траектории
и оптимальной фазовой траектории 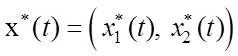 воспользуемся уравнениями Эйлера.
воспользуемся уравнениями Эйлера.
Составим функцию Лагранжа
![]() .
.
Получаем задачу безусловной оптимизации с теми же граничными условиями (6.2) и (6.3) в виде функционала
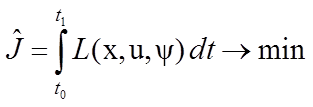 .
(6.4)
.
(6.4)
Применяем уравнения Эйлера
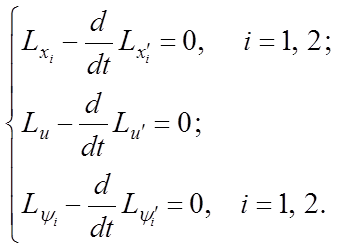
к функционалу (6.4). Вычисляем соответствующие производные уравнений Эйлера:
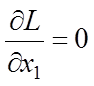 ,
,
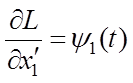 ,
, 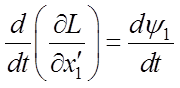 ,
,
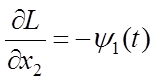 ,
, 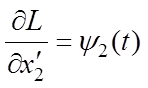 ,
, 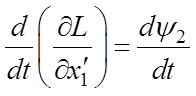 ,
,
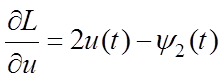 ,
, 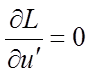 ,
,
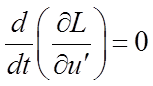 ,
,
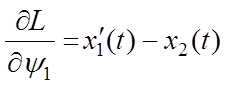 ,
, 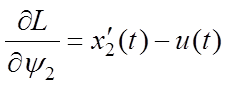 .
.
Подставляя найденные величины в уравнения Эйлера, получим систему уравнений
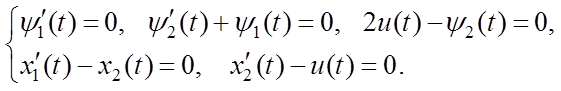 (6.5)
(6.5)
Решая систему (6.5), последовательно находим:
![]() ,
, ![]() ,
,
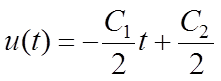 ,
(6.6)
,
(6.6)
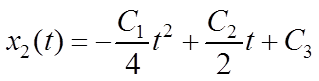 ,
(6.7)
,
(6.7)
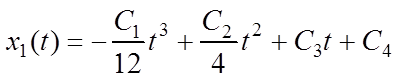 .
(6.8)
.
(6.8)
Для определения постоянных интегрирования ![]() ,
, ![]() ,
, ![]() и
и ![]() в (6.6)
– (6.8) используем граничные условия (6.2) и (6.3) при
в (6.6)
– (6.8) используем граничные условия (6.2) и (6.3) при ![]() ,
,
![]() . После несложных вычислений находим:
. После несложных вычислений находим:
![]() ,
, 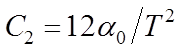 ,
, ![]() ,
, ![]() .
.
Следовательно, для заданных граничных условий можно окончательно
записать уравнения оптимальных процессов 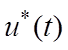 ,
, 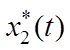 и
и 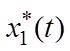
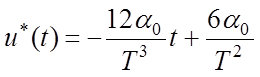 ,
, 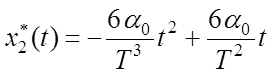 , (6.9)
, (6.9)
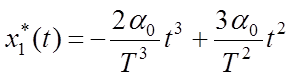 .
.
Графики 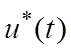 и
и ![]() , соответствующие формулам (6.9), приведены
на рис. 6.1.
, соответствующие формулам (6.9), приведены
на рис. 6.1.
Как видно из рис. 6.1, управляющее воздействие ![]() (ток якоря двигателя) должно меняться по
линейному закону, а скорость поворота вала двигателя
(ток якоря двигателя) должно меняться по
линейному закону, а скорость поворота вала двигателя 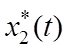 –
по параболе, где
–
по параболе, где ![]() – заданный угол поворота вала
двигателя.
– заданный угол поворота вала
двигателя.
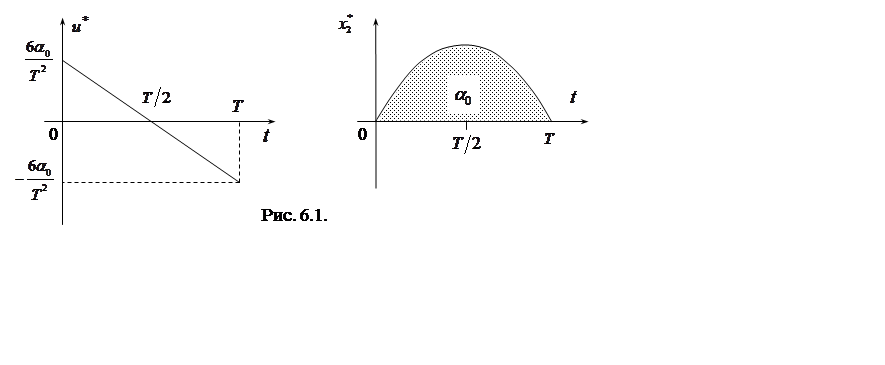 |
Пример 6.2.
На основании примера 6.1 при той же постановке задачу оптимального управления рассмотрим влияние ограничения по скорости в следующем виде
![]() ,
, ![]() (5.43)
(5.43)
на решение задачи.
Таким образом, можем исследовать решение задачи в
примере 5.1 с учетом условия (6.10). Из (6.9) следует, что решение относительно
переменной ![]() должно удовлетворять условию
должно удовлетворять условию
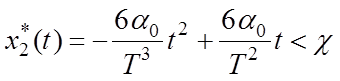 .
(6.11)
.
(6.11)
Если условие (6.11) не выполняется, то ![]() ,
, ![]() и
и ![]() не являются решениями поставленной задачи.
Иначе говоря, если имеет место условие
не являются решениями поставленной задачи.
Иначе говоря, если имеет место условие ![]() , то
оптимальная траектория
, то
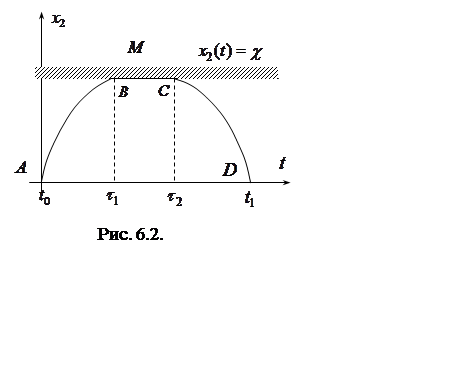
оптимальная траектория ![]() состоит из трех частей (рис.
6.2): одна часть
состоит из трех частей (рис.
6.2): одна часть ![]() лежит вне запрещенной области
лежит вне запрещенной области ![]() и поэтому имеет форму квадратной параболы
(6.7)
и поэтому имеет форму квадратной параболы
(6.7)
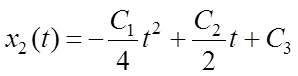 ;
;
вторая
часть ![]() также принадлежит области допустимых
значений для
также принадлежит области допустимых
значений для ![]() и поэтому будет иметь форму квадратной
параболы, но с другими коэффициентами:
и поэтому будет иметь форму квадратной
параболы, но с другими коэффициентами:
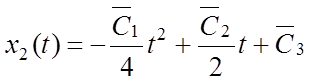 ;
;
третья
часть ![]() (рис. 6.2) совпадает с границей области
(рис. 6.2) совпадает с границей области ![]() , поэтому
, поэтому
![]()
и соединяет первые две части.
 |
Обозначим через ![]() и
и ![]() те моменты времени
те моменты времени ![]() ,
когда сопрягаются указанные части оптимальной траектории. Эти моменты пока еще
неизвестны и подлежат определению.
,
когда сопрягаются указанные части оптимальной траектории. Эти моменты пока еще
неизвестны и подлежат определению.
В соответствии с (6.6) - (6.8) оптимальный процесс имеет вид:
1)
на отрезке времени ![]() :
:
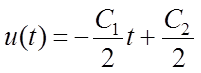 ,
,
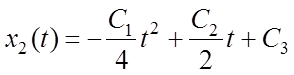 ,
(6.12)
,
(6.12)
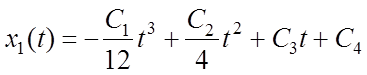 ;
;
2)
на отрезке времени ![]() :
:
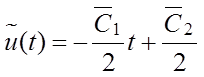 ,
,
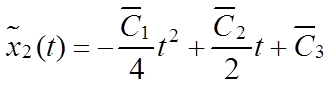 ,
(6.13)
,
(6.13)
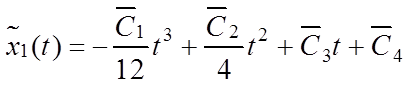 ;
;
3)
на отрезке времени ![]() :
:
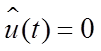 ,
, 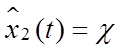 ,
, 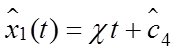 .
(6.14)
.
(6.14)
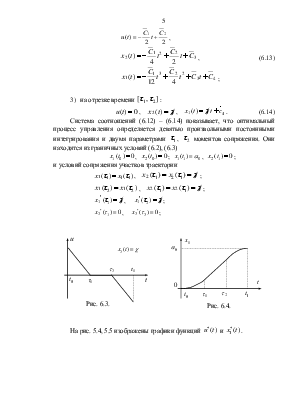
Система соотношений (6.12) – (6.14) показывает, что
оптимальный процесс управления определяется девятью произвольными постоянными интегрирования
и двумя параметрами ![]() ,
, ![]() моментов
сопряжения. Они находятся из граничных условий (6.2), (6.3)
моментов
сопряжения. Они находятся из граничных условий (6.2), (6.3)
![]() ,
, ![]() ;
; ![]() ,
, ![]() ;
;
и условий сопряжения участков траектории
![]() ,
, 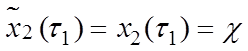 ;
;
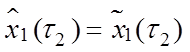 ,
, 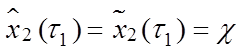 ;
;
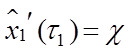 ,
, 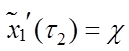 ;
;
 ,
, ![]() ;
;
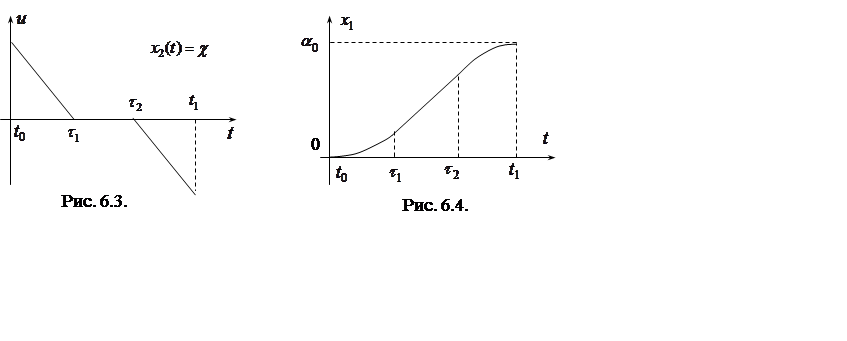 |
На рис. 5.4, 5.5 изображены графики функций ![]() и
и ![]() .
.
Список рекомендуемой литературы.
1. Атанс М., Фалб П. Оптимальное управление. М., «Машиностроение», 1968.
2. Беллман Р., Калаба Р. Динамическое программирование и современная теория управления. –М.: Наука, 1969.
3. Болтянский В.Г. Математические методы оптимального управления. –М.: Наука, 1968.
4. Брайсон А., Хо Ю-ши Прикладная теория оптимального управления. Оптимизация, оценка и управление. М.: Мир, 1972. –544 с.
5. Нефедов Ю.М. Теория управления. Учеб. пос. –Луганск: Изд-во ВНУ им. В.Даля, 2003. – 228 с.
6. Петров Ю.П. Вариационные методы теории оптимального управления. – Л.: Энергия, 1977. – 280 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.