Методи розв'язання лінійних систем диференціальних рівнянь з постійними коефіцієнтами, страница 3

3) додаткова умова: характеристичний многочлен кожної діагональної клітки являє собою степінь не приводимого у поле K многочлена.

З останнього маємо, що якщо K – поле  чисел, то серед елементарних дільників можуть бути степеня квадратних тричленів, що не приводяться, з дійсними коефіцієнтами, а у випадку комплексного поля чисел всі елементарні дільники мають вигляд  двочленів Якщо числове поле K - комплексне, те елементарні дільники мають вигляд          

(j = 1,2,…,u)                                              (2.33)

де – характеристичні числа й .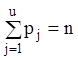

Розглянемо питання кількості (числа) елементарних дільників, що відповідають даному характеристичному числу. Вище встановлено, що в комплексному полі K матриця  n-го порядку має елементарні дільники виду (2.33), сума показників степенів яких дорівнює n. Із цього треба, що інваріантні многочлени (2.25) матриці мають вигляд двочленів (2.33), тобто:

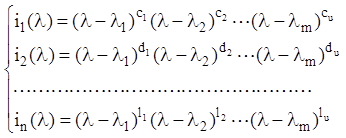                                 (2.34)

 (k = 1,2,…,u)

де  (j = 1,…,u) можуть мати деякі з показників  (k = 1,…,u) рівними нулю. Якщо врахувати, що

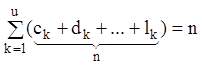
то легко бачити, що багато показників степенів з  дорівнюють нулю, а самі степені лінійних двочленів дорівнюють одиниці.

Оскільки характеристичне рівняння  може мати не більше n різних характеристичних чисел (тільки у випадку простих характеристичних чисел їхнє число дорівнює n), то число s всіх елементарних дільників . З огляду на канонічний  діагональний вид матриці  (див. 2.26)

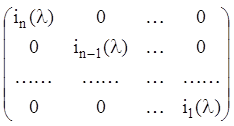                                           (2.35)

і структуру її елементів (2.34), можна визначити число її елементарних дільників для кожного характеристичного числа (j = 1,…,u)...

Дійсно, поклавши в канонічній матриці (2.35) , ряд її діагональних елементів, починаючи з нижнього, звернеться в нуль, тому що в нуль звернуться елементарні дільники, що відповідають цьому характеристичному числу . Очевидно, що число елементарних дільників

,                                                                 (2.36)

де – відповідний ранг канонічної діагональної матриці при .

Розглядаючи дану матрицю  й з огляду на її еквівалентність із канонічної квазідіагональної матрицею містимо про рівність рангу матриці  при з рангом . Тому формулу (2.36) можна записати у вигляді:

 (j = 1,2,…,n),                                                   (2...37)

де – ранг матриці ().

Таким чином, для кожного характеристичного числа (j = 1,2,…,u£n) квадратної матриці A n-го порядку існує група елементарних дільників виду яка складається згідно (2.37), з елементарних дільників. Ця група може включати один або кілька елементарних дільників залежно від їхніх ступенів і кратності розглянутого характеристичного числа .

Зокрема, якщо для розглянутий  ранг , то, згідно (2.37), число елементарних дільників . У випадку простого характеристичного числа кратності k = 1 це буде простий (степеня ) елементарний дільник:

У випадку k-кратного характеристичного числа цей елементарний дільник буде степеня , тобто:

.

Якщо матриця  рангу  й  – кратне характеристичне число, то число елементарних дільників , тобто характеристичне число кратності k має k простих елементарних дільників:

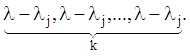
Варто підкреслити, що простим характеристичним числам матриці A завжди відповідають прості елементарні дільники.

Визначивши число елементарних дільників для кожного характеристичного числа (j = 1,2,…,u£n) і додавши їх, знайдемо число S всіх елементарних дільників матриці A, тобто 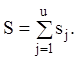З огляду на (2.37) останню рівність можна записати у вигляді:

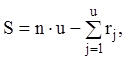                                                     (2.38)

де u – число різних характеристичних чисел матриці A, – ранги матриць

Отже, підводячи підсумки в питанні про знаходження елементарних дільників матриці, відзначаємо наступне: якщо матриця A n-го порядку має в загальному випадку кілька характеристичних чисел (j = 1,2,…,u£n), причому відповідної кратності – натуральні числа, кожне з яких не менше 1, а їхня сума то побудувавши відповідні кожному із цих чисел елементарні дільники, одержимо сукупність всіх елементарних дільників матриці A:

                                       (2.39)

де S – їхнє загальне число. При цьому очевидно, що показники степенів – натуральні числа, кожне з яких не менше 1, а їхня сума Крім того, відомо, що кратному характеристичному числу може відповідати кілька елементарних дільників, тому й серед чисел можуть бути рівні.

Розглянемо приклади знаходження елементарних дільників заданих матриць.

Приклад 1. Знайти елементарні дільники матриці:

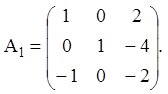
Розв’язання. Знаходимо характеристичні числа матриці A, розв’язавши рівняння:

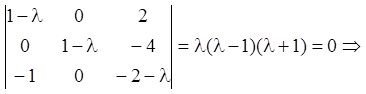
Таким чином, характеристичні числа всі прості. Ранг матриць (j = 1,2,3) дорівнює 2. Тоді Отже, всі елементарні дільники будуть простими: