


Лекция №1
Тема: Интегральное исчисление. Неопределенный интервал.
F(х)→f`'(х); f(х)→F(х); F'(х)=f(х)
ПР. F(х²)=х² F(х)=![]() ; F(х)=
; F(х)= 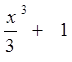 ; F(х)
; F(х) 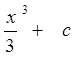 ; }:F(х)=f(х)
; }:F(х)=f(х)
Def. Функция F(х) называется первообразной от данной функции f(х), если ее производная F'(х)совпадает с данной функцией f(х) или, что тоже, ее дифференциал равен f (х)dx:
{F(х)- первообразная от f (х)}⇔{F'(х)=f(х); df=f(x)dx} (1)
Теорема Любая непрерывная на интервале (а,в) функция, производная которой во всех точках этого интервала равна нулю, есть ? на этом интервале.
![]()
![]() ? ∀х∈(а,в): F`(x)=0⇒∀х1,х2
∈(а,в): F(х2)-F(х1)=F`(λ)(х2-х1)
? ∀х∈(а,в): F`(x)=0⇒∀х1,х2
∈(а,в): F(х2)-F(х1)=F`(λ)(х2-х1)
λ∈(х1:х2) //
⇒F(х2)-F(х1)=0⇒∀х1,х2∈(а,в):F(х1)=F(х2)⇒F(х)=consf
Если F(х) есть некоторая первообразная от функции f(х) то любая другая первообразная функции Ф(х) от f(х) будет отличатся от F(х) лишь на константу, т.е.
![]()
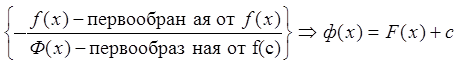
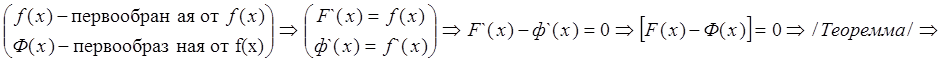
![]()
![]() Следовательно: Выражение { } охватывает совокупность всех превообразных функций f(x). Определение: Множество функций Ф(х)=F(х)+с, где
F(х)- есть некоторая первообразная от функции f(х), а с=const называется неопределенным интегралом
от функции f(х) и обозначается
Следовательно: Выражение { } охватывает совокупность всех превообразных функций f(x). Определение: Множество функций Ф(х)=F(х)+с, где
F(х)- есть некоторая первообразная от функции f(х), а с=const называется неопределенным интегралом
от функции f(х) и обозначается
![]()
![]() (2)
(2)
Действие отыскания неопределенного интеграла от функции f(х) называется интегрированием этой функции.
Пример: f(х)=х²;⇒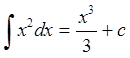
Свойства неопределенного интеграла.
1. ∫f(х)dx=F(x)+c⇒[∫f(x)dx]`=[F(x)+c]`=f`(x)=f(x)
/производная от неопределенного интеграла равна ? функции/;
2. ∫f(х)dx=F(x)+c⇒d[∫f(x)dx]`·dx= f(x)dx
/Дифференциал от неопределенного интеграла равен подинтегральному выражению/.
3. Неопределенный интеграл линеен относительно интегрируемых функций:
а) 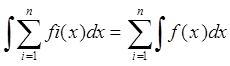 ;
;
б) ∫kf(x)dx=C∫f(x)dx, Где k=consf
4. Неопределенный интеграл от дифференциала некоторой функции равен этой функции + consf
∫f(x)dx=F(x)+c⇒F`(x)=f(x)⇒dF=F`(x)dx=f(x)dx⇒∫dF=F+c
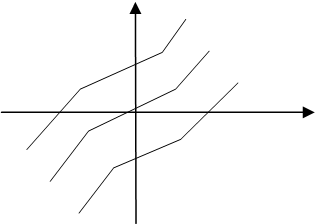
5. Геометрический смысл. Def График первообразной у=F(х) от функции f(х) называется интегрированной кривой.
у=F(х)⇒∫f(х)○ f(х)=tgλ
Геометрическое интегрирование функции f(х) сводится к построению семейства интегрированных кривых, если известен тангенс угла ? касательной в каждой точке этих кривых.
F(х)=tg2⇒λ=arctgf(x)- поле прерываний.
 |
 Пример Через точку М(1,2) провести кривую, у которой ? коэффициент касательной в
каждой точке с абцисой х равен f(х)=х²
Пример Через точку М(1,2) провести кривую, у которой ? коэффициент касательной в
каждой точке с абцисой х равен f(х)=х²
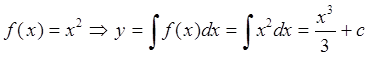 .
.
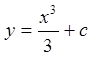 ; м(1,2)⇒2=
; м(1,2)⇒2=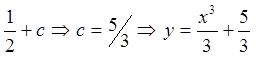
искомая кривая.
Методы интегрирования.
1. Метод непосредственного интегрирования. Основан на использовании свойства неопределенного интеграла и таблицы:
1.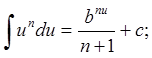 n≠-1; ∫du=u+c;
n≠-1; ∫du=u+c; 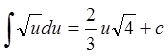
2. 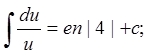 3.
3. 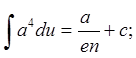 ∫e4du=e4+c
∫e4du=e4+c
4.∫sinudu=-cosutc 5. ∫cosudu= sinu +c
6. 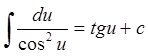 7.
7. 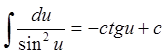
8. .∫shudu=chu+c; 9. ∫ shudu=shu+c
10. 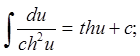 11.
11. 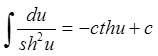
12. 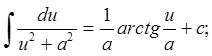 13.
13. ![]()
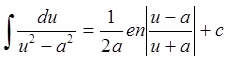
14. 15.
15. 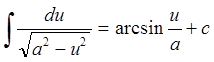
Пример 1 1) 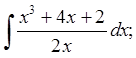 2)
2)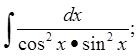
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.