






































МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
ИМЕНИ ВЛАДИМИРА ДАЛЯ
Кафедра «ПРИКЛАДНАЯ МАТЕМАТИКА»
Специальность 080202 - «ПРИКЛАДНАЯ МАТЕМАТИКА»
МЕТОДИЧЕСКАЯ ДОКУМЕНТАЦИЯ
по дисциплине «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ (общий курс)»
Документ №8
«Индивидуальные семестровые задачи
самостоятельной работы»
I.
1)
![]()
2)
![]()
3)
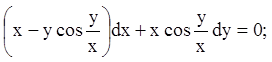
4)
![]()
5)
![]()
6)
![]()
7)
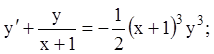
8)
![]()
9)
![]()
10) 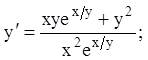
11) 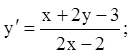
12) ![]()
13) ![]()
14) ![]()
15) ![]()
16) 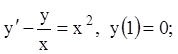
17) ![]()
18) ![]()
19) ![]()
20) ![]()
21) 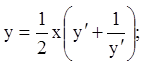
22) 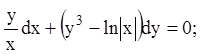
23) ![]()
24) ![]()
25) ![]()
26) ![]()
27) ![]()
28) ![]()
29) 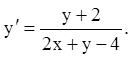
II.
1)
Материальная точка массы ![]() движется по
прямолинейному пути к центру, притягивающему ее с силой
движется по
прямолинейному пути к центру, притягивающему ее с силой ![]() ,
где
,
где ![]() - расстояние точки от центра. Движение
начинается с состояния покоя при
- расстояние точки от центра. Движение
начинается с состояния покоя при ![]() . Найти время, по
истечении которого точка достигнет центра.
. Найти время, по
истечении которого точка достигнет центра.
2)
Зависимость между углом наклона ![]() скорости потока газа к
оси
скорости потока газа к
оси ![]() и величиной этой скорости
и величиной этой скорости ![]() можно записать следующим дифференциальным
уравнением:
можно записать следующим дифференциальным
уравнением:
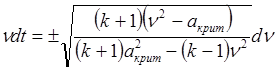 , где
, где ![]() – постоянные. Найти
– постоянные. Найти ![]() .
.
III.
1)
![]()
2)
![]()
I.
1)
![]()
2)
![]()
3)
![]()
4)
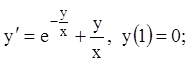
5)
![]()
6)
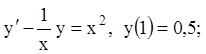
7)
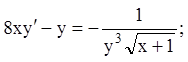
8)
![]()
9)
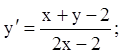
10)
![]()
11)
![]()
12)
![]()
13)
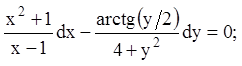
14)
![]()
15)
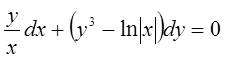
16)
![]()
17)
![]()
18)
![]()
19)
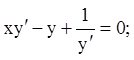
20)
![]()
21)
![]()
22)
![]()
23)
![]()
24)
![]()
25)
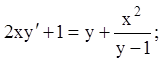
26)
![]()
27)
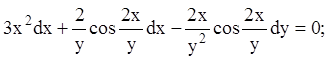
28)
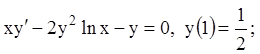
29)
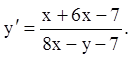
II.
1) Скорость распада радия пропорциональна наличному его количеству. В течение года из каждого грамма радия распадается 0,44 мг. Через сколько лет распадется половина имеющегося количества радия?
2)
Определить полный магнитный поток катушки, равномерно намотанной на сердечник
прямоугольного сечения, внутренний радиус которого ![]() см;
наружный –
см;
наружный – ![]() см;
высота
см;
высота ![]() см;
см; ![]() А;
число витков
А;
число витков ![]() (сердечник из магнитодиэлектрика).
Величина потока удовлетворяет уравнению:
(сердечник из магнитодиэлектрика).
Величина потока удовлетворяет уравнению:
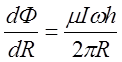 .
.
III.
1)
![]()
2)
![]()
I.
1)
![]()
2)
![]()
3)
![]()
4)
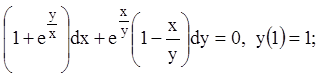
5)
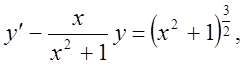
6)
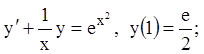
7)
![]()
8)
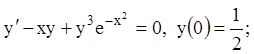
9)
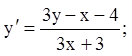
10)
![]()
11)
![]()
12)
![]()
13)
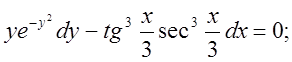
14)
![]()
15)
![]()
16)
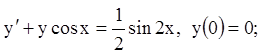
17)
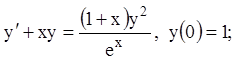
18)
![]()
19)
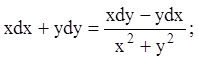
20)
![]()
21)
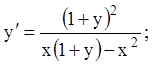
22)
![]()
23)
![]()
24)
![]()
25)
![]()
26)
![]()
27)
![]()
28)
![]()
29)
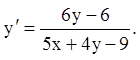
II.
1)
Скорость размножения некоторых бактерий пропорциональна их количеству в
рассматриваемый момент времени ![]() . Количество бактерий
утроилось за 5ч. Найти зависимость количества бактерий от времени.
. Количество бактерий
утроилось за 5ч. Найти зависимость количества бактерий от времени.
2)
Количество вещества, входящего в химическую реакцию через ![]() секунд после ее начала, равно
секунд после ее начала, равно ![]() . Найти
. Найти ![]() , если
скорость реакции
, если
скорость реакции 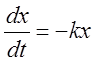 , где
, где ![]() –
постоянная и
–
постоянная и ![]() .
.
III.
1)
![]()
2)
![]()
I.
1)
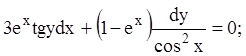
2)
![]()
3)
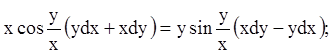
4)
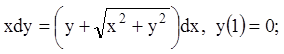
5)
![]()
6)
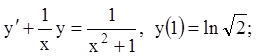
7)
![]()
8)
![]()
9)
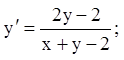
10)
![]()
11)
![]()
12)
![]()
13)
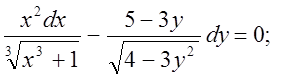
14)
![]()
15)
![]()
16)
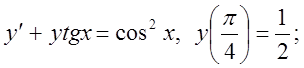
17)
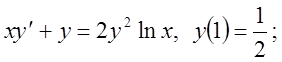
18)
![]()
19)
![]()
20)
![]()
21)
![]()
22)
![]()
23)
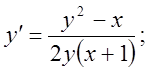
24)
![]()
25)
![]()
26)
![]()
27)
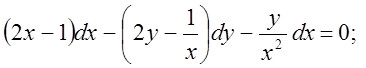
28)
![]()
29)
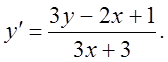
II.
1)
Лодку разгоняют в спокойной воде до скорости ![]() , после
чего выключают двигатель. Сопротивление воды пропорционально скорости. Описать
дальнейшее движение лодки. Найти время движения до остановки и пройденный путь.
, после
чего выключают двигатель. Сопротивление воды пропорционально скорости. Описать
дальнейшее движение лодки. Найти время движения до остановки и пройденный путь.
2)
Одно из основных уравнений термодинамики (уравнение изохор), выражающее
зависимость постоянной равновесия ![]() от теплового эффекта
от теплового эффекта ![]() и температуры
и температуры ![]() реакции,
представляется в виде:
реакции,
представляется в виде: 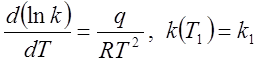 , где
, где ![]() – число калорий, выделяющихся в процессе
реакции;
– число калорий, выделяющихся в процессе
реакции; ![]() – абсолютная температура. Найти уравнение
изохоры.
– абсолютная температура. Найти уравнение
изохоры.
III.
1)
![]()
2)
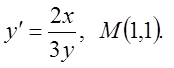
I.
1)
![]()
2)
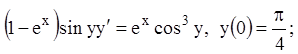
3)
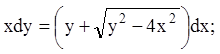
4)
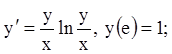
5)
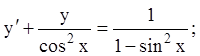
6)
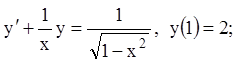
7)
![]()
8)
![]()
9)
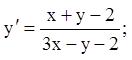
10)
![]()
11)
![]()
12)
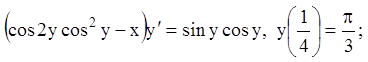
13)
![]()
14)
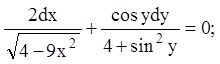
15)
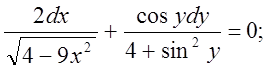
16)
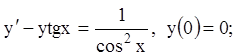
17)
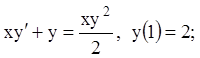
18)
![]()
19)
![]()
20)
![]()
21)
![]()
22)
![]()
23)
![]()
24)
![]()
25)
![]()
26)
![]()
27)
![]()
28)
![]()
29)
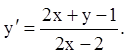
II.
1)
Ракета перед стартом имеет массу ![]() кг. На какой высоте
окажется ракета через 15с после начала работы ее двигателей? Считать расход
топлива
кг. На какой высоте
окажется ракета через 15с после начала работы ее двигателей? Считать расход
топлива ![]() кг/с, скорость истечения газов
относительно ракеты
кг/с, скорость истечения газов
относительно ракеты ![]() м/с постоянными; поле тяготения
Земли однородно.
м/с постоянными; поле тяготения
Земли однородно.
2)
Для средней области интенсивности ощущений имеет место психофизический закон
соотношения между ощущением Е и раздражением 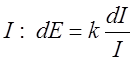 .
Определить
.
Определить ![]() , если
, если ![]() –
постоянная.
–
постоянная.
III.
1)
![]()
2)
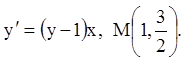
I.
1)
![]()
2)
![]()
3)
![]()
4)
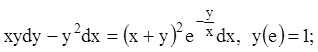
5)
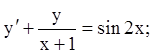
6)
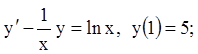
7)
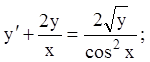
8)
![]()
9)
![]()
10)
![]()
11)
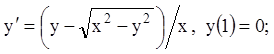
12)
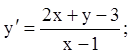
13)
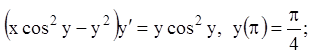
14)
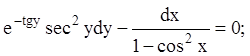
15)
![]()
16)
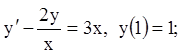
17)
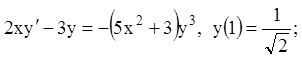
18)
![]()
19)
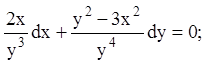
20)
![]()
21)
![]()
22)
![]()
23)
![]()
24)
![]()
25)
![]()
26)
![]()
27)
![]()
28)
![]()
29)
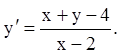
II.
1)
Температура вынутого из печи каравая хлеба в течение 20 мин падает от ![]() до
до ![]() .
Температура воздуха равна
.
Температура воздуха равна ![]() . Через сколько времени
от начала момента охлаждения температура хлеба понизилась до
. Через сколько времени
от начала момента охлаждения температура хлеба понизилась до ![]() ?
?
2)
Мальчик бежал на коньках по льду со скоростью 15 км/ч. Через ![]() с он остановился, пробежав
с он остановился, пробежав ![]() м. Его скорость в момент времени
м. Его скорость в момент времени ![]() выражалась формулой
выражалась формулой 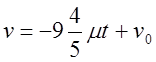 , где
, где ![]() –
начальная скорость в м/с, а
–
начальная скорость в м/с, а ![]() – коэффициент трения
между коньками и поверхностью льда. Определить
– коэффициент трения
между коньками и поверхностью льда. Определить ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.