




Контрольна робота № 7
«Функції декількох змінних»
Задача 1. Знайти й зобразити область визначення
функції ![]() .
.
1.1. 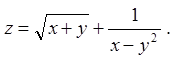 1.2.
1.2.
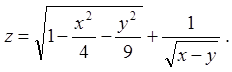
1.3. 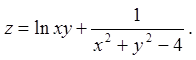 1.4.
1.4.
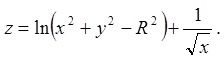
1.5. 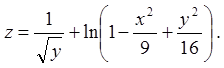 1.6.
1.6.
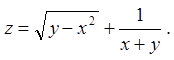
1.7. ![]() 1.8.
1.8.
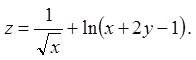
1.9. 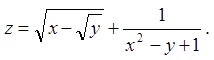 1.10.
1.10.
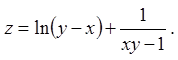
Задача 2. Обчислити границі функцій.
2.1. 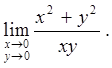 2.2.
2.2.
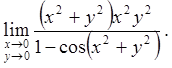
2.3. 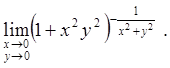 2.4.
2.4.
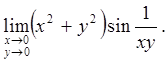
2.5. 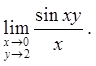 2.6.
2.6.
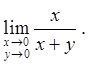
2.7. 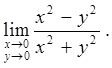 2.8.
2.8.
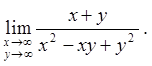
2.9. 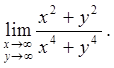 2.10.
2.10.
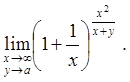
Задача 3.
3.1. Показати, що функція ![]() задовольняє рівнянню
Лапласа:
задовольняє рівнянню
Лапласа: 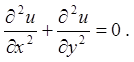
3.2. Показати, що функція ![]() задовольняє рівнянню
Лапласа:
задовольняє рівнянню
Лапласа:
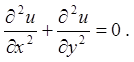
3.3. Показати, що функція 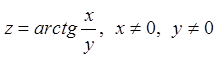 задовольняє рівнянню
Лапласа:
задовольняє рівнянню
Лапласа:
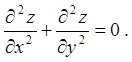
3.4. Показати, що функція 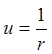 , де
, де ![]() задовольняє рівнянню Лапласа:
задовольняє рівнянню Лапласа:
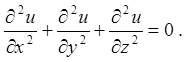
3.5. Показати, що функція 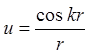 , де
, де ![]() , задовольняє рівнянню Гельмгольца:
, задовольняє рівнянню Гельмгольца: 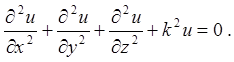
3.6. Показати, що функція 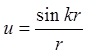 , де
, де ![]() , задовольняє рівнянню Гельмгольца:
, задовольняє рівнянню Гельмгольца: 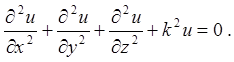
3.7. Показати, що функція ![]() , де
, де ![]() , а
, а ![]() –
довільні константи, задовольняє бігармонічному рівнянню Максвела:
–
довільні константи, задовольняє бігармонічному рівнянню Максвела: 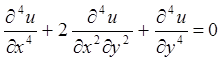 .
.
3.8. Показати, що функція ![]() , де
, де ![]() – довільні двічі диференційовані функції,
задовольняє хвильовому рівнянню:
– довільні двічі диференційовані функції,
задовольняє хвильовому рівнянню: 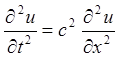 .
.
3.9. Нехай функція ![]() задовольняє
телеграфному рівнянню :
задовольняє
телеграфному рівнянню : 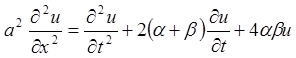 . Якому рівнянню
задовольняє функція
. Якому рівнянню
задовольняє функція ![]() ? Яким буде це рівняння, якщо
? Яким буде це рівняння, якщо ![]() ?
?
3.10. Показати, що функція 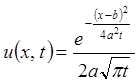 задовольняє рівнянню
теплопровідності:
задовольняє рівнянню
теплопровідності: 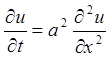 .
.
Задача 4. Знайти частинні похідні вказаних порядків.
4.1. 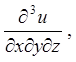 якщо
якщо 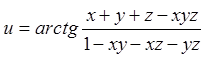 . 4.2.
. 4.2.
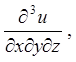 якщо
якщо ![]() .
.
4.3. 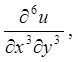 якщо
якщо ![]() . 4.4.
. 4.4.
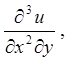 якщо
якщо ![]() .
.
4.5. 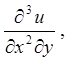 якщо
якщо ![]() . 4.6.
. 4.6.
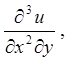 якщо
якщо 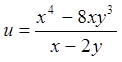 .
.
4.7. 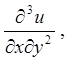 якщо
якщо ![]() . 4.8.
. 4.8.
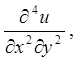 якщо
якщо ![]() .
.
4.9. 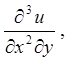 якщо
якщо ![]() . 4.10.
. 4.10.
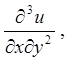 якщо
якщо 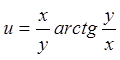 .
.
Задача 5. Замінюючи приріст функції її диференціалом, обчислити наближено.
5.1. 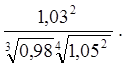 5.2.
5.2.
![]()
5.3. ![]() 5.4.
5.4.
![]()
5.5. ![]() 5.6.
5.6.
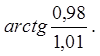
5.7. ![]() 5.8.
5.8.
![]()
5.9. ![]() 5.10.
5.10.
![]()
Задача 6. Знайти повні диференціали першого і другого порядків від функцій.
6.1. 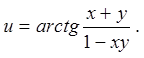 6.2.
6.2.
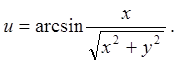
6.3. ![]() 6.4.
6.4.
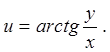
6.5. 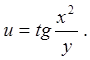 6.6.
6.6.
![]()
6.7. ![]() 6.8.
6.8.
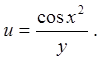
6.9. 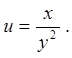 6.10.
6.10.
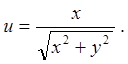
Задача 7. Знайти повні диференціали першого і другого
порядків від складних функцій (![]() – незалежні змінні).
– незалежні змінні).
7.1. ![]() , де
, де ![]() . 7.2.
. 7.2.
![]() , де
, де ![]() .
.
7.3. 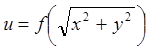 . 7.4.
. 7.4.
![]() , де
, де ![]() .
.
7.5. ![]() . 7.6.
. 7.6.
![]() , де
, де ![]() .
.
7.7. ![]() , де
, де ![]() . 7.8.
. 7.8.
![]() , де
, де ![]() .
.
7.9. ![]() . 7.10.
. 7.10.
![]() .
.
Задача 8. Для функції ![]() знайти
градієнт в точці
знайти
градієнт в точці ![]() і похідну в точці
і похідну в точці ![]() за напрямком вектора
за напрямком вектора ![]() .
.
8.1.
![]()
8.2.
![]()
8.3.
![]()
8.4.
![]()
8.5.
![]()
8.6.
![]()
8.7.
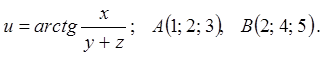
8.8.
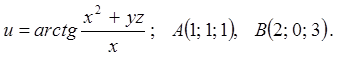
8.9.
![]()
8.10.
![]()
Задача 9. Знайти похідну ![]() функції
заданої неявно.
функції
заданої неявно.
9.1. ![]() . 9.2.
. 9.2.
![]() .
.
9.3. 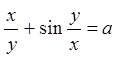 . 9.4.
. 9.4.
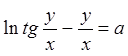 .
.
9.5. ![]() . 9.6.
. 9.6.
![]() .
.
9.7. 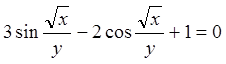 . 9.8.
. 9.8.
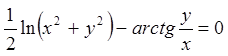 .
.
9.9. 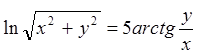 . 9.10.
. 9.10.
![]() .
.
Задача 10. Знайти частинні похідні 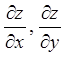 функції
функції ![]() заданої
неявно.
заданої
неявно.
10.1. ![]() . 10.2.
. 10.2.
![]() .
.
10.3. ![]() . 10.4.
. 10.4.
![]() .
.
10.5. 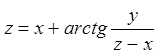 . 10.6.
. 10.6.
![]() .
.
10.7. ![]() . 10.8.
. 10.8.
![]() .
.
10.9. ![]() . 10.10.
. 10.10.
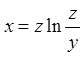 .
.
Задача 11. Написати рівняння дотичної площини і
рівняння нормалі до поверхні в даній точці ![]() .
.
11.1. ![]() . 11.2.
. 11.2.
![]() .
.
11.3. ![]() . 11.4.
. 11.4. 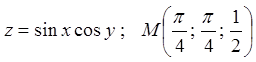 .
.
11.5. ![]() . 11.6.
. 11.6. 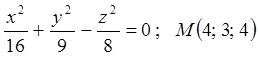 .
.
11.7. ![]() . 11.8.
. 11.8. ![]() .
.
11.9. ![]() . 11.10.
. 11.10. 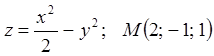 .
.
Задача 12. Дослідити на екстремум функцію.
12.1. 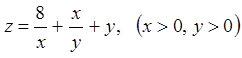 . 12.2.
. 12.2. ![]() .
.
12.3. 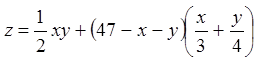 . 12.4.
. 12.4. ![]() .
.
12.5. ![]() . 12.6.
. 12.6.
![]() .
.
12.7. ![]() . 12.8.
. 12.8. ![]() .
.
12.9. ![]() . 12.10.
. 12.10. ![]() .
.
Задача 13. Знайти умовні екстремуми функції.
13.1. ![]() при
при
![]() . 13.2.
. 13.2.
![]() при
при ![]() .
.
13.3. ![]() при
при
![]() . 13.4.
. 13.4.
![]() при
при ![]() .
.
13.5. ![]() при
при
![]() . 13.6.
. 13.6.
![]() при
при 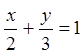 .
.
13.7. ![]() при
при
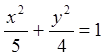 . 13.8.
. 13.8.
![]() при
при 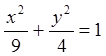 .
.
13.9. 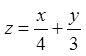 при
при
![]() . 13.10.
. 13.10.
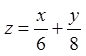 при
при 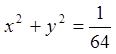 .
.
Задача 14. Знайти найбільше і найменше значення функції
![]() в області
в області ![]() .
.
14.1. 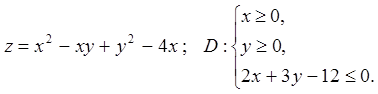 14.2.
14.2. ![]()
14.3. 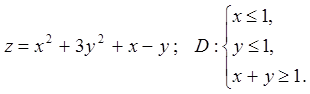 14.4.
14.4. 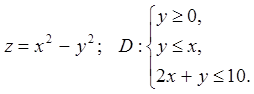
14.5. ![]() 14.6.
14.6. 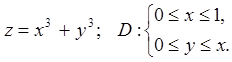
14.7. 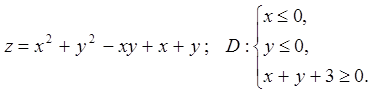 14.8.
14.8. ![]()
14.9. 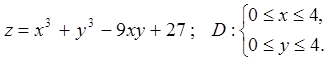 14.10.
14.10. 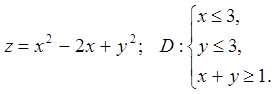
Задача 15.
15.1. Виготовити з жерсті, з найменшими затратами матеріалу, прямокутну коробку (без кришки) заданої місткості
15.2. В дану кулю діаметра ![]() вписати прямокутний
паралелепіпед найбільшого об’єму.
вписати прямокутний
паралелепіпед найбільшого об’єму.
15.3. Знайти розміри циліндричної посудини найбільшої місткості з
заданою площею поверхні ![]() .
.
15.4. Сума ребер прямокутного паралелепіпеда дорівнює ![]() . Які розміри має паралелепіпед найбільшого
об’єму?
. Які розміри має паралелепіпед найбільшого
об’єму?
15.5. Знайти прямокутний паралелепіпед найбільшого об’єму за умови, що
довжина його діагоналі дорівнює ![]() .
.
15.6. Знайти конус (обертання) даного об’єму ![]() з
найменшою повною поверхнею.
з
найменшою повною поверхнею.
15.7. В кулю діаметра ![]() вписати циліндр з
найменшою повною поверхнею.
вписати циліндр з
найменшою повною поверхнею.
15.8. З усіх прямокутних паралелепіпедів з даною повною поверхнею ![]() знайти той, який має найбільший об’єм.
знайти той, який має найбільший об’єм.
15.9. Визначити розміри конуса найбільшого об’єму за умови, що його
бокова поверхня дорівнює ![]() .
.
15.10. Серед усіх прямокутних трапецій, одна з бічних сторін яких
лежить на відрізку ![]() , а конці іншої на графіці
, а конці іншої на графіці ![]() , знайти ту, що має найбільшу площу.
, знайти ту, що має найбільшу площу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.