







План:
1. Диференціювання випадкового процесу.
1.1. Визначення диференційованого випадкового процесу і його характеристики.
1.2. Необхідна умова диференційованості випадкового процесу.
1.3. Достатня умова диференційованості випадкового процесу.
2. Інтегрування випадкового процесу.
2.1. Визначення інтеграла від випадкового процесу.
2.2. Імовірностні характеристики інтеграла від випадкового процесу.
Визначення. Випадковий процес ![]() називається диференційованим у
середньоквадратичному в т.
називається диференційованим у
середньоквадратичному в т.![]() , якщо існує
среднеквадратический межа виду
, якщо існує
среднеквадратический межа виду
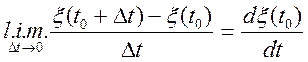 (6.1)
(6.1)
Межа (6.1) називають среднеквадратической
похідній від випадкового процесу. Якщо ця похідна існує в будь-якій крапці ![]() деякого інтервалу, то випадковий процес
називається диференційованим на інтервалі.
деякого інтервалу, то випадковий процес
називається диференційованим на інтервалі.
Нехай задані вероятностные
характеристики випадкового процесу ![]() . Знайдемо вероятностные
характеристики похідної випадкового процесу
. Знайдемо вероятностные
характеристики похідної випадкового процесу ![]() .
Знайдемо мат. чекання від обох частин рівності (6.1), використовуючи
властивості мат. чекання:
.
Знайдемо мат. чекання від обох частин рівності (6.1), використовуючи
властивості мат. чекання:
1) мат. чекання від межі дорівнює межі мат. чекань;
2) невипадковий множник може бути винесений за знак мат. чекання.
Тоді
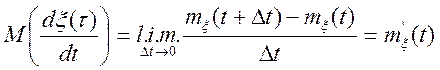 . (6.2)
. (6.2)
Т.е. мат. чекання похідній дорівнює похідній мат. чекання.
Введемо в розгляд випадковий процес ![]()
![]() . Використовуючи
визначення центрованого випадкового процесу
. Використовуючи
визначення центрованого випадкового процесу ![]() ,
одержуємо
,
одержуємо
![]() .
(6.3)
.
(6.3)
Дійсно,
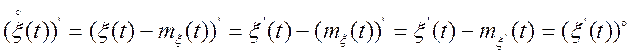 .
.
На підставі (6.3) можна змінювати місцями операції центрування випадкового процесу і диференціювання.
Визначимо взаємно кореляційні функції
для двох випадкових процесів ![]() і
і ![]() , приймаючи в увагу безперервність
кореляційної функції
, приймаючи в увагу безперервність
кореляційної функції ![]() для безперервного випадкового
процесу.
для безперервного випадкового
процесу.
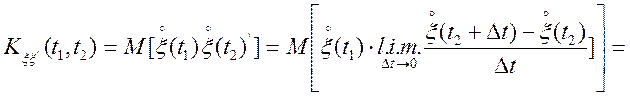
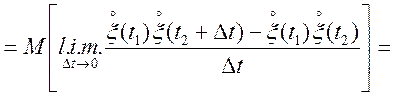
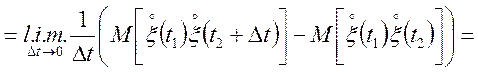
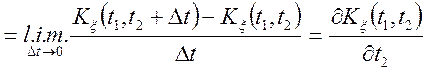 .
.
Отже,
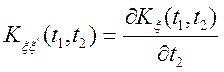 .
(6.4)
.
(6.4)
Аналогічно, можна одержати
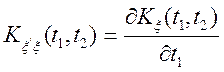 . (6.5)
. (6.5)
Перейдемо до обчислення кореляційної функції похідній випадкового процесу. На підставі
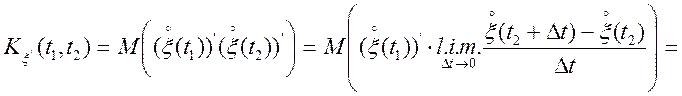
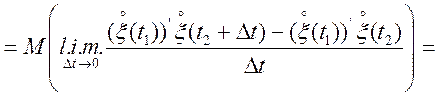
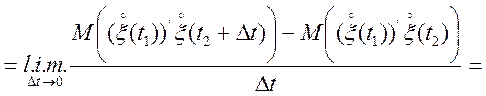
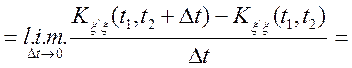
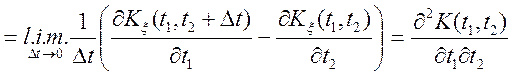 .
.
Отже,
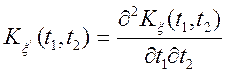 (6.6)
(6.6)
Т.о. доведені теоретично дифференцируемость математичного чекання випадкового процесу й існування другої похідної від кореляційної функції є необхідна умова дифференцируемости випадкового процесу.
Можна також сформулювати і достатня умова дифференцируемости.
Теорема. Для того, щоб випадковий процес ![]() був диференціюємо, досить щоб було
дифференцируемо його мат. чекання
був диференціюємо, досить щоб було
дифференцируемо його мат. чекання ![]() й існувала при
й існувала при ![]() друга змішана похідна від
друга змішана похідна від ![]() .
.
Приклад.
Показати, що узагальнений телеграфний сигнал не є дифференцируемым.
![]() ,
, ![]() .
.
Знайдемо ![]() і
і ![]() .
.
![]() ;
;
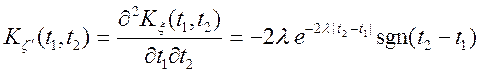
т.о. 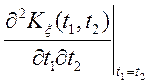 має два значення
значить випадковий процес не диференціюємо
має два значення
значить випадковий процес не диференціюємо
Приклад.
Чи буде диференціюємо ![]() , якщо
, якщо ![]() , де
, де ![]() і
і ![]() невипадкові величини, а
невипадкові величини, а ![]() випадкова величина з щільністю розподілу
випадкова величина з щільністю розподілу 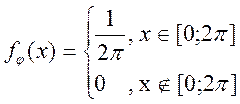
Рішення.
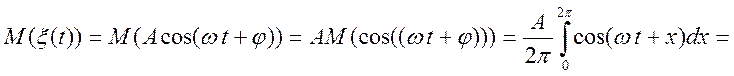
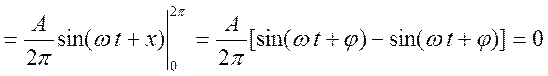 .
.
![]() отже
отже ![]() .
.
По визначенню ![]() знайдемо
знайдемо
![]()
![]()
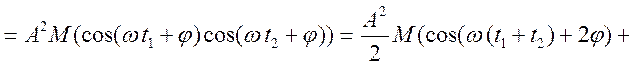
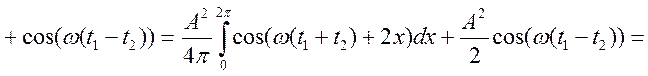
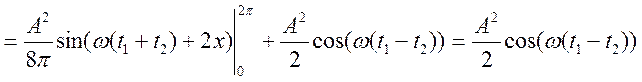
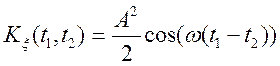
![]()
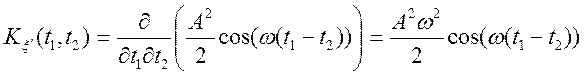
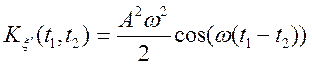
при ![]() ,
, 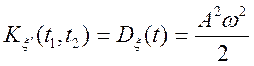 ,
виходить, процес
,
виходить, процес ![]() диференціюємо.
диференціюємо.
Розглянемо невипадкову функцію від двох перемінних ![]() . Припустимо, що
. Припустимо, що ![]() кусочно-непререрывная
функція по обох перемінним на відрізку
кусочно-непререрывная
функція по обох перемінним на відрізку ![]() і
випадковий процес
і
випадковий процес ![]() безперервний для кожного
безперервний для кожного ![]() . Розіб'ємо
. Розіб'ємо ![]() тоді
тоді ![]() , для кожного
, для кожного ![]() .
.
Назвемо розбивку правильним, якщо ![]() , при
, при ![]() .
.
Побудуємо суму виду
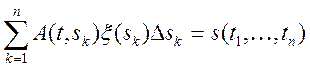 .
.
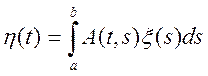 (6.7)
(6.7)
Назвемо ![]() інтегралом у середньо
квадратичному від випадкового процесу
інтегралом у середньо
квадратичному від випадкового процесу ![]() (інтегральним
оператором), якщо існує межа в змісті середньо квадратичного від інтегральної
суми на безлічі правильних розбивок
(інтегральним
оператором), якщо існує межа в змісті середньо квадратичного від інтегральної
суми на безлічі правильних розбивок
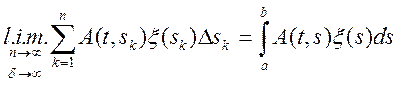 .
.
Функцію ![]() називають ядром інтегрального
оператора. В окремому випадку інтеграл випадкового процесу
називають ядром інтегрального
оператора. В окремому випадку інтеграл випадкового процесу ![]() за умови
за умови 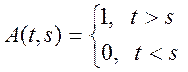 прийме
прийме
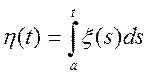 .
(6.8)
.
(6.8)
Зауваження.
Існування середньо квадратического межі означає виконання умови
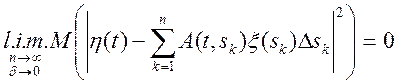 .
.
Виразимо числові характеристики випадкового процесу ![]() через числові характеристики
через числові характеристики ![]() (формули (6.7) або (6.8)).
(формули (6.7) або (6.8)).
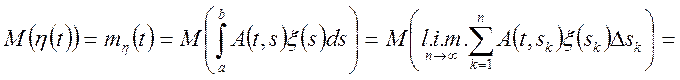
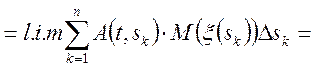
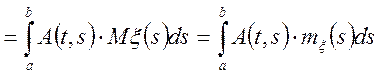
![]()
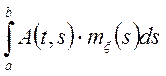 (6.9)
(6.9)
В окремому випадку (6.8)
![]()
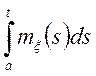 (6.10)
(6.10)
Таким чином, математичне чекання інтеграла від випадкового процесу дорівнює інтегралові від математичного чекання.
Знайдемо кореляційну функцію від випадкового процесу ![]() через
через ![]() .
.
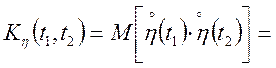
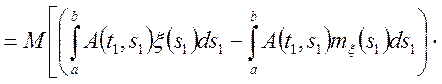
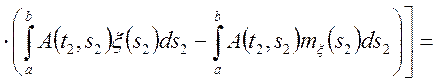
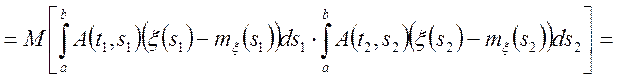
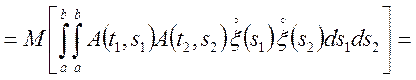
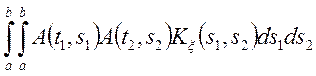
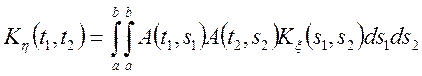 (6.11)
(6.11)
В окремому випадку
![]()
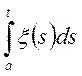
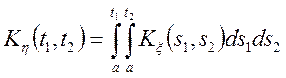 (6.12)
(6.12)
Теорема. Кореляційна функція інтеграла від випадкового процесу дорівнює подвійному інтегралові від кореляційної функції вихідного випадкового процесу інтеграла, що коштує під знаком.
Або ж, якщо процес ![]() інтегруємо
на
інтегруємо
на ![]() , тобто має місце (6.7), те интегрируемы і
його числові характеристики.
, тобто має місце (6.7), те интегрируемы і
його числові характеристики.
Справедлива і зворотна теорема.
Теорема. Якщо числові характеристики випадкового процесу ![]() интегрируемы на
интегрируемы на ![]() ,
то і самому процесі
,
то і самому процесі ![]() інтегруємо.
інтегруємо.
Приклад.Випадкові процеси ![]() і
і ![]() зв'язані співвідношенням
зв'язані співвідношенням
![]()
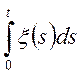 .
.
Знайти: ![]() ,
, ![]() ,
, ![]() , якщо
, якщо ![]() ,
, ![]() .
.
Рішення.
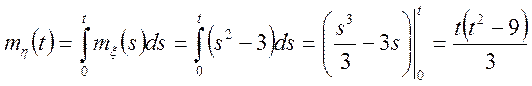
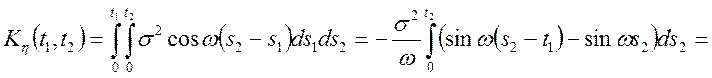
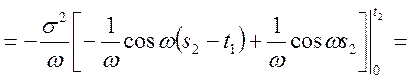
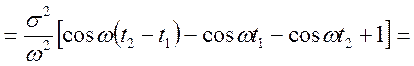
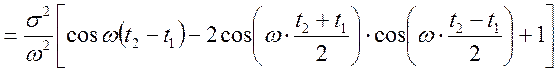 .
.
![]()
![]()
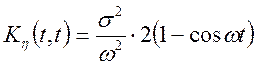 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.