a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
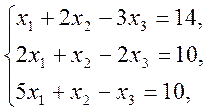2) 
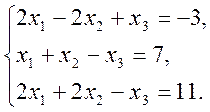3)
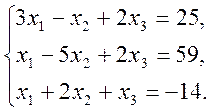
3. Написати розкладення вектору 
за векторами 
, 
, 
:
, 
, 
, 
.
Варіант 14
1. Обчислити визначники:
а)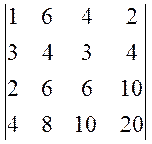 
, б) 
.
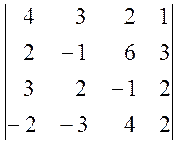2. Розв’язати СЛАР (систему лінійних алгебраїчних рівнянь):
a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
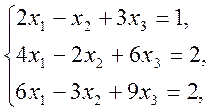2) 
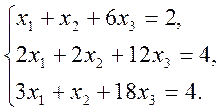3)
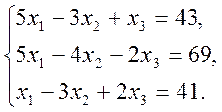
3. Написати розкладення вектору за векторами , , :
, 
, 
, 
.
Варіант 15
1. Обчислити визначники:
а)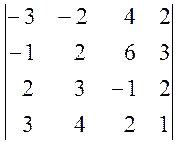 
, б) 
.
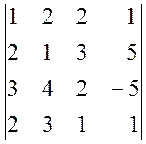2. Розв’язати СЛАР (систему лінійних алгебраїчних рівнянь):
a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
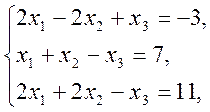2) 
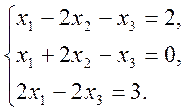3)
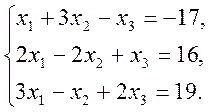
3. Написати розкладення вектору за векторами , , :
, 
, 
, 
.
Варіант 16
1. Обчислити визначники:
а)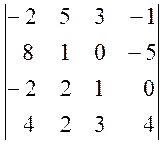 
, б) 
.
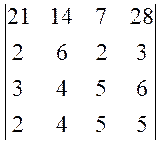2. Розв’язати СЛАР (систему лінійних алгебраїчних рівнянь):
a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
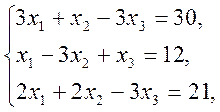2) 
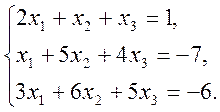3)
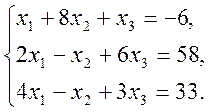
3. Написати розкладення вектору за векторами , , :
, 
, 
, 
.
Варіант 17
1. Обчислити визначники:
а)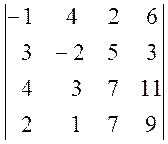 
, б) 
.
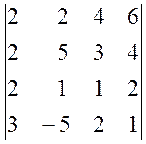2. Розв’язати СЛАР (систему лінійних алгебраїчних рівнянь):
a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
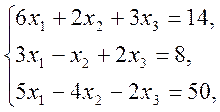2) 
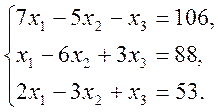3)
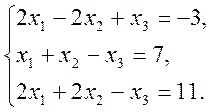
3. Написати розкладення вектору за векторами , , :
, 
, 
, 
.
Варіант 18
1. Обчислити визначники:
а)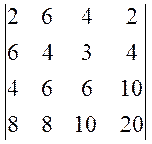 
, б) 
.
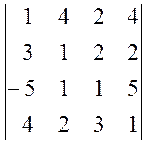2. Розв’язати СЛАР (систему лінійних алгебраїчних рівнянь):
a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
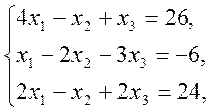2) 
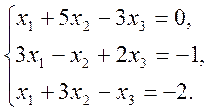3)
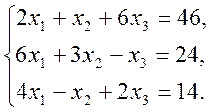
3. Написати розкладення вектору за векторами , , :
, 
, 
, 
.
Варіант 19
1. Обчислити визначники:
а)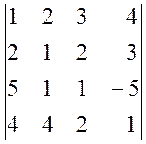 
, б) 
.
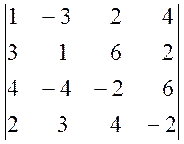2. Розв’язати СЛАР (систему лінійних алгебраїчних рівнянь):
a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
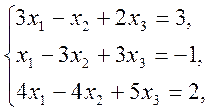2) 
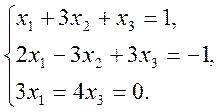3)
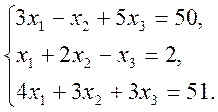
3. Написати розкладення вектору за векторами , , :
, 
, 
, 
.
Варіант 20
1. Обчислити визначники:
а)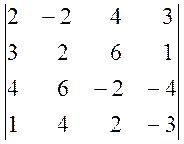 
, б) 
.
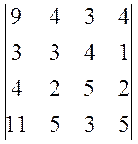2. Розв’язати СЛАР (систему лінійних алгебраїчних рівнянь):
a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
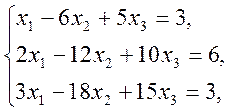2) 
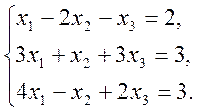3)
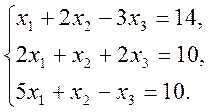
3. Написати розкладення вектору за векторами , , :
, 
, 
, 
.
Варіант 21
1. Обчислити визначники:
а)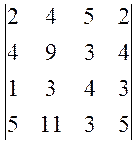 
, б) 
.
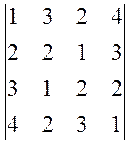2. Розв’язати СЛАР (систему лінійних алгебраїчних рівнянь):
a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
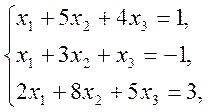2) 
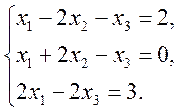3)
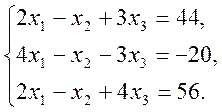
3. Написати розкладення вектору за векторами , , :
, 
, 
, 
.
Варіант 22
1. Обчислити визначники:
а)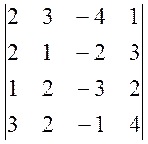 
, б) 
.
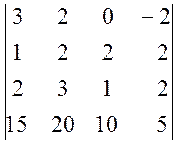2. Розв’язати СЛАР (систему лінійних алгебраїчних рівнянь):
a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
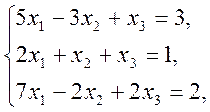2) 
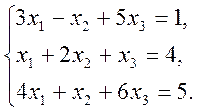3)
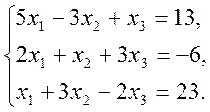
3. Написати розкладення вектору за векторами , , :
, 
, 
, 
.
Варіант 23
1. Обчислити визначники:
а)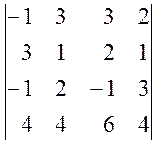 
, б) 
.
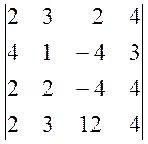2. Розв’язати СЛАР (систему лінійних алгебраїчних рівнянь):
a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
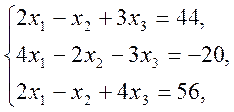2) 
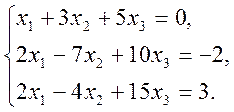3)
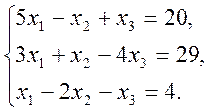
3. Написати розкладення вектору за векторами , , :
, 
, 
, 
.
Варіант 24
1. Обчислити визначники:
а)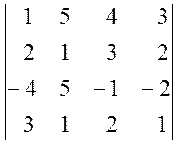 
, б) 
.
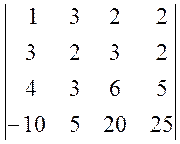2. Розв’язати СЛАР (систему лінійних алгебраїчних рівнянь):
a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
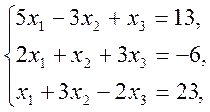2) 
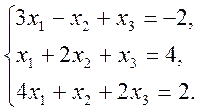3)
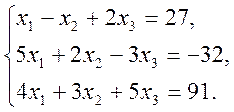
3. Написати розкладення вектору за векторами , , :
, 
, 
, 
.
Варіант 25
1. Обчислити визначники:
a)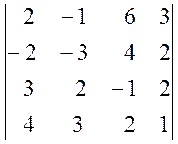 
, b)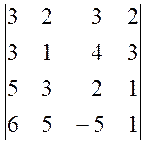 
.
2. Розв’язати СЛАР (систему лінійних алгебраїчних рівнянь):
a) методом Крамера;
b) засобами матричного обчислення;
c) методом Гауса.
1) 
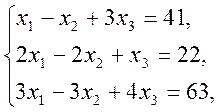2) 
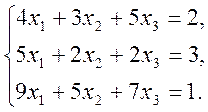3)
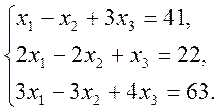
3. Написати розкладення вектору за векторами , , :
, 
, 
, 
.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
Кафедра «ПРИКЛАДНА МАТЕМАТИКА»
КОНТРОЛЬНА РОБОТА № 2
З дисципліни «вища математика для економістів(I)»
Луганськ, 2004
Варіант№1
1. Привести квадратичну форму до канонічного виду
2. Знайти рівняння геометричного місця точок, відстань котрих від початку
координат й від точки 
відносяться один до одного як
2:1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.