Анализ линейных систем управления: Практическое занятие № 2

Практическое занятие  2.

Тема: Анализ линейных систем управления.

Цель занятия :  Временные характеристики одномерных систем. Преобразование Лапласа. Решение систем линейных дифференциальных уравнений. Передаточные функции линейной одномерной системы с постоянными параметрами. Решение типовых задач.

Пример 2.1.

Пусть изображение   .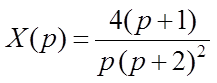

Пользуясь формулой разложения, определить оригинал.

Решение. Согласно принятым обозначениям:

;  .

Функция  имеет полюсы (т.е. корни уравнения ) . Полюс  является простым, а полюс – кратным, имея кратность . На основании теоремы разложения (2.39) имеем

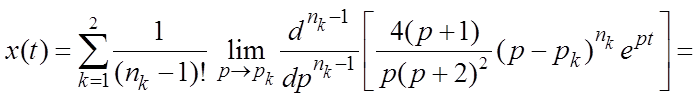
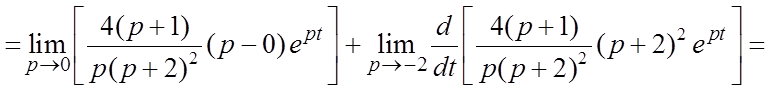
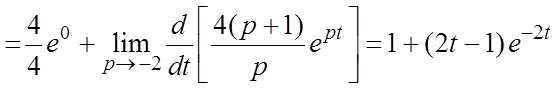
Таким образом, .

Для простейших дробно–рациональных функций на основании формулы разложения можно построить более простые формулы определения оригиналов.

Пусть

,

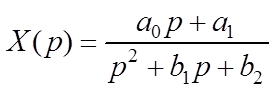где , , ,  – постоянные вещественные числа.

Знаменатель дроби изображения  можно представить в виде

.

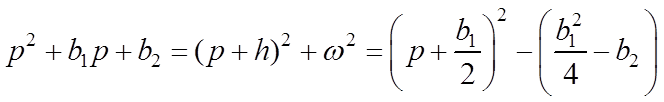Возможны три случая.

1.  Корни знаменателя комплексные, т.е.  Тогда

,

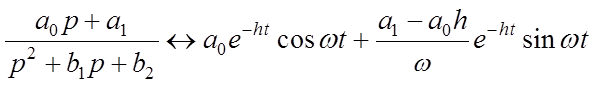где ,  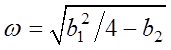 . Эти обозначения использованы в 2 и 3.

2.  Корни знаменателя вещественные, т.е. . Тогда

,

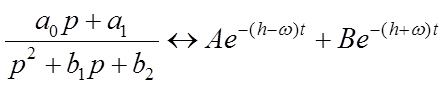где , .

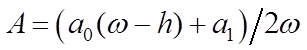3.  Корни знаменателя равные, т.е. . Тогда

.

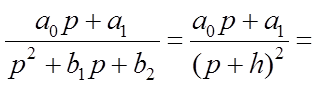
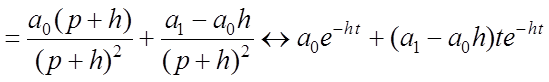Преобразования Лапласа широко используются для решения обыкновенных дифференциальных уравнений. Этот математический аппарат можно непосредственно использовать для вычисления импульсной переходной матрицы следующим образом. Используем принятое обозначение для преобразования Лапласа функции : . Тогда, согласно теории этого преобразования, если функция  дифференцируема, то

где   .

Рассмотрим стационарную однородную систему

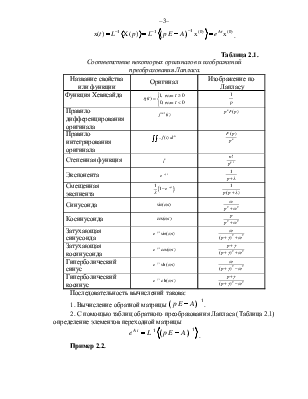
и ее преобразование Лапласа

Тогда

    или    .

Матрица 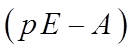 является характеристической матрицей матрицы , которая является неособенной при всех , где  – характеристические числа матрицы . Следовательно, выражение  имеет смысл при всех . Взяв обратное преобразование Лапласа, найдем

.

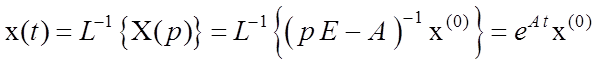Таблица 2.1.

Соответствие некоторых оригиналов и изображений

 преобразования Лапласа.

Название свойства или функции		Оригинал		Изображение по  Лапласу
	Функция Хевисайда
Правило дифференцирования оригинала
Правило интегрирования оригинала
Степенная функция
Экспонента
Смещенная экспнента
Синусоида
Косинусоида
Затухающая синусоида
Затухающая косинусоида
Гиперболический синус
Гиперболический косинус

Последовательность вычислений такова:

1.  Вычисление обратной матрицы .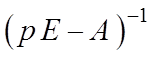

2.  С помощью таблиц обратного преобразования Лапласа (Таблица 2.1) определение элементов переходной матрицы

.

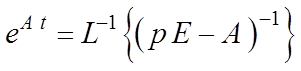Пример 2.2.

Пусть система 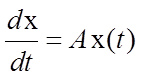 имеет матрицу 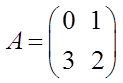. Построить импульсную переходную матрицу.

Характеристическая матрица: .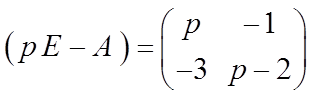

Вычисляем обратную матрицу. При этом определитель исходной матрицы:   . После несложных преобразований обратная матрица будет иметь следующий вид:

.

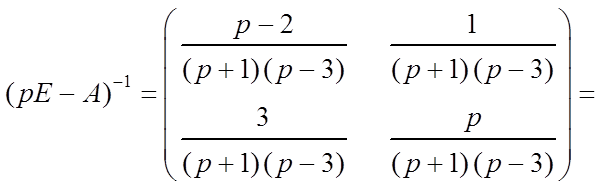
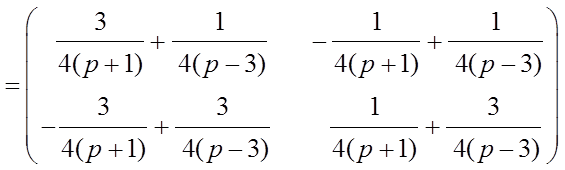Пользуясь таблицей обратного преобразования Лапласа (Таблица 2.1), получим

.

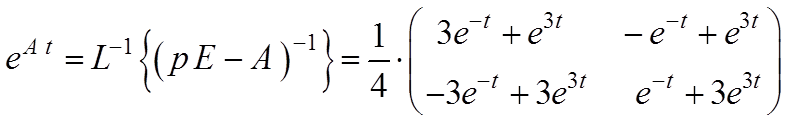Пример 2.3.

Рассмотрим однородное дифференциальное уравнение в нормальной форме

,

где   ,   ,   .

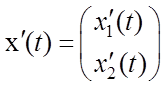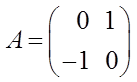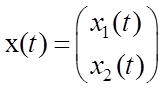Найти решение при заданных начальных условиях .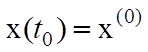

Решение.

Импульсная переходная матрица для этой системы удовлетворяет уравнению

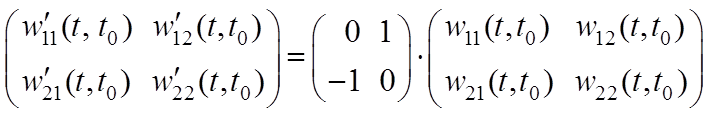
при начальном условии .

Ряд Пеано для вычисления  в этом примере легко суммируется потому, что выявляется закономерность суммирования матриц :  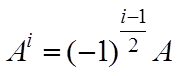для  нечетных и 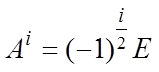 для  четных. Например,

,

,

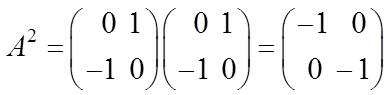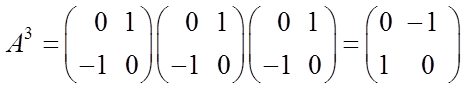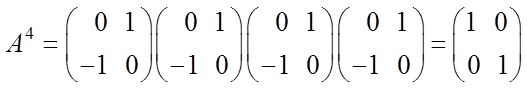 и т.д.

Простое вычисление показывает, что

,

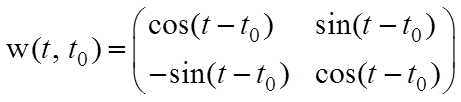где использованы разложения тригонометрических функций в ряд Тейлора

 

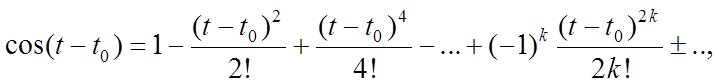
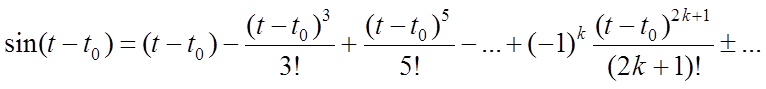
Следовательно,

,

.

Список рекомендуемой литературы.

1.  Атанс М., Фалб П. Оптимальное управление. М., «Машиностроение», 1968.

2.  Беллман Р., Калаба Р. Динамическое программирование и современная теория управления. –М.: Наука, 1969.

3.  Болтянский В.Г. Математические методы оптимального управления. –М.: Наука, 1968.

4.  Брайсон А., Хо Ю-ши Прикладная теория оптимального управления. Оптимизация, оценка и управление. М.: Мир, 1972. –544 с.

5.  Нефедов Ю.М. Теория управления. Учеб. пос. –Луганск: Изд-во ВНУ им. В.Даля, 2003. – 228 с.