





Лекція 13
План:
1. Автокореляційна функція.
2. Рішення типових прикладів.
Визначення. Кореляційної (або «автокореляційної»)
функцією випадкової функції ![]() називається невипадкова функція
двох аргументів
називається невипадкова функція
двох аргументів ![]() , що при кожній парі значень
аргументів
, що при кожній парі значень
аргументів ![]() ,
, ![]() дорівнює
кореляційному моментові відповідних перетинів випадкової функції:
дорівнює
кореляційному моментові відповідних перетинів випадкової функції:
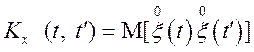 ,
(13.1)
,
(13.1)
де 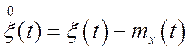 – центрована випадкова функція.
– центрована випадкова функція.
При ![]() кореляційна
функція перетворюється в дисперсію випадкової функції:
кореляційна
функція перетворюється в дисперсію випадкової функції:
![]() (13.2)
(13.2)
Основні властивості кореляційної функції:
![]() , тобто функція
, тобто функція ![]() не міняється при заміні
не міняється при заміні ![]() на
на ![]() (симетричність);
(симетричність);
![]() ;
;
функція ![]() –
позитивно визначена тобто
–
позитивно визначена тобто 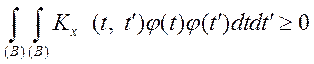 , де
, де ![]() – будь-яка функція,
– будь-яка функція, ![]() – будь-яка область інтегрування, однакова
для обох аргументів.
– будь-яка область інтегрування, однакова
для обох аргументів.
Для нормальної випадкової функції
характеристики ![]() ,
, ![]() є вичерпними
і визначать собою закон розподілу будь-якого числа перетинів.
є вичерпними
і визначать собою закон розподілу будь-якого числа перетинів.
Нормованою кореляцією випадкової
функції ![]() називається функція
називається функція
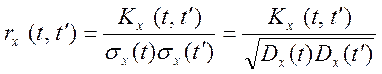 , (13.3)
, (13.3)
т. е. коефіцієнт кореляції перетинів ![]() і
і ![]() ; при
; при ![]()
![]() .
.
Випадковий процес ![]() називається
процесом з незалежними збільшеннями, якщо для будь-яких значень аргументу
називається
процесом з незалежними збільшеннями, якщо для будь-яких значень аргументу ![]() випадкові величини збільшення функції
випадкові величини збільшення функції ![]()
![]() ;
; ![]() ; ...;
; ...; ![]() (13.4)
(13.4)
незалежні.
Визначення. Нормальний випадковий процес з незалежними збільшеннями називається винеровським випадковим процесом, якщо його математичне чекання дорівнює нулеві, а дисперсія збільшення пропорційна довжині відрізка, на якому воно досягає:
![]() ;
; ![]() ,
(13.5)
,
(13.5)
де ![]() —
постійний коефіцієнт.
—
постійний коефіцієнт.
При додатку до
випадкової функції ![]() невипадкового доданка
невипадкового доданка ![]() до її
математичного чекання додається той же невипадковий доданок, а кореляційна
функція не міняється.
до її
математичного чекання додається той же невипадковий доданок, а кореляційна
функція не міняється.
При множенні
випадкової функції ![]() на невипадковий множник
на невипадковий множник ![]() її
математичне чекання збільшується на той же множник
її
математичне чекання збільшується на той же множник ![]() , а
кореляційна функція – на
, а
кореляційна функція – на ![]() .
.
Якщо випадкову
функцію ![]() піддають деякому перетворенню
піддають деякому перетворенню ![]() , то
виходить інша випадкова функція
, то
виходить інша випадкова функція ![]() .
.
Перетворення ![]() називається
лінійним однорідним
називається
лінійним однорідним
1) 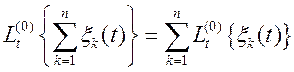
(т. е. перетворення до суми може застосовуватися почленно);
2) ![]()
(т. е. множник ![]() , незалежно від аргументу
, незалежно від аргументу ![]() , по якому вироблятися перетворення,
можна виносити за знак перетворення).
, по якому вироблятися перетворення,
можна виносити за знак перетворення).
Перетворення ![]() називається
лінійним неоднорідним, якщо
називається
лінійним неоднорідним, якщо
![]() ,
,
де ![]() — не
випадкова функція.
— не
випадкова функція.
Якщо випадкова функція ![]() зв'язана з випадковою функцією
зв'язана з випадковою функцією ![]() лінійним
перетворенням
лінійним
перетворенням ![]() ., те її математичне чекання
., те її математичне чекання ![]() виходить з
виходить з ![]() тем же
лінійним перетворенням:
тем же
лінійним перетворенням:
![]() , (13.6)
, (13.6)
а для перебування кореляційної
функції ![]() потрібно двічі піддано функцію
потрібно двічі піддано функцію ![]() відповідному лінійному однорідному
перетворенню: один раз по
відповідному лінійному однорідному
перетворенню: один раз по ![]() інший раз по
інший раз по ![]() :
:
![]() . (13.7)
. (13.7)
Взаємною кореляційною функцією ![]() двох випадкових функцій
двох випадкових функцій ![]() і
і ![]() називається функція
називається функція
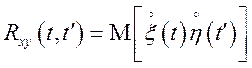 . (13.8)
. (13.8)
З визначення взаємної кореляційної функції випливає, що
![]() .
.
Нормованою взаємною кореляційною
функцією двох випадкових функцій ![]() і
і ![]() називається функція
називається функція
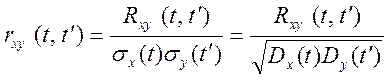 .
(13.9)
.
(13.9)
Випадкові функцій ![]() і
і ![]() називаються
некорелірованими, якщо
називаються
некорелірованими, якщо
![]() .
.
Якщо ![]() , то
, то ![]() ,
,
![]() .
.
Якщо випадкові функції ![]() і
і ![]() некореліровані, то
некореліровані, то
![]() .
(13.10)
.
(13.10)
Якщо
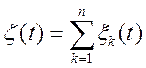 , (13.11)
, (13.11)
де ![]() ,
, ![]() , …...,
, …..., ![]() –
некореліровані випадкові функції, тоді
–
некореліровані випадкові функції, тоді
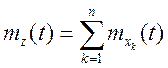 ,
, 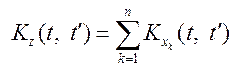 .
.
При виконанні різних перетворень з випадковими функціями часто буває зручно записувати них у комплексному виді. Комплексною випадковою функцією називається випадкова функція виду
![]() ,
(13.12)
,
(13.12)
де ![]() ,
, ![]() — дійсні випадкові функції,
— дійсні випадкові функції, ![]() — мнима одиниця.
— мнима одиниця.
Математичне чекання, кореляційна функція і дисперсія комплексної випадкової функції визначаються в такий спосіб:
![]() ,
, 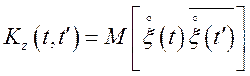 ,
(13.13)
,
(13.13)
де чорної вгорі позначена комплексна сполучена величина, а
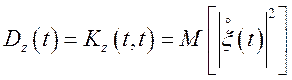 .
(13.14)
.
(13.14)
При переході до комплексних випадкових величин і функцій необхідно визначати дисперсію як математичне чекання квадрата модуля, а кореляційний момент — як математичне чекання добутку центрованої однієї випадкової величини на комплексну сполучену центрованою дугою.
Задачі даного
параграфа![]() належать до двох основних типів. У задачах
першого типу потрібно визначити кореляційну функцію випадкової функції,
використовуючи властивості її ординат, або установити загальні властивості
кореляційної функції. При рішенні цих задач потрібно безпосередньо виходити з
визначення кореляційної функції. У задачах другого типу потрібно знайти
імовірність того, що ординати нормальної випадкової функції приймуть визначені
значення. Для рішення цих задач необхідно скористатися відповідним нормальним
законом розподілу, обумовленим математичним чеканням і кореляційною функцією.
належать до двох основних типів. У задачах
першого типу потрібно визначити кореляційну функцію випадкової функції,
використовуючи властивості її ординат, або установити загальні властивості
кореляційної функції. При рішенні цих задач потрібно безпосередньо виходити з
визначення кореляційної функції. У задачах другого типу потрібно знайти
імовірність того, що ординати нормальної випадкової функції приймуть визначені
значення. Для рішення цих задач необхідно скористатися відповідним нормальним
законом розподілу, обумовленим математичним чеканням і кореляційною функцією.
Приклад 1. Визначити кореляційну
функцію ![]() , якщо
, якщо
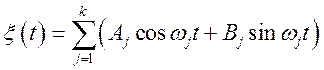 ,
,
де ![]() —
задані числа, а речовинні випадкові величини
—
задані числа, а речовинні випадкові величини ![]() і
і ![]() , взаємно не коррелированны, мають нульові
математичні чекання і дисперсії, обумовлені рівностями
, взаємно не коррелированны, мають нульові
математичні чекання і дисперсії, обумовлені рівностями
![]() (j=1,2,…,k)
(j=1,2,…,k)
Рішення. Тому що 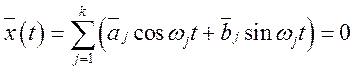 , те по визначенню кореляційної функції
, те по визначенню кореляційної функції
![]()
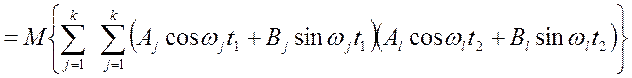 .
.
Розкриваючи дужки
і застосовуючи теорему про математичне чекання, зауважуємо, що всі доданки, що
містять множники виду ![]() при j≠ l і
при j≠ l і ![]() при будь-яких j і l
дорівнюють нулеві, а
при будь-яких j і l
дорівнюють нулеві, а ![]() . Тому
. Тому
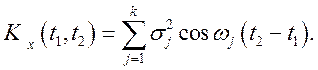
Приклад 2. Нехай ![]() — нормальна стаціонарна випадкова функція,
математичне чекання якої дорівнює нулеві. Довести що якщо
— нормальна стаціонарна випадкова функція,
математичне чекання якої дорівнює нулеві. Довести що якщо
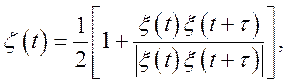
те
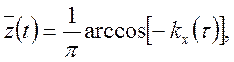
де ![]() – нормована кореляційна функція
– нормована кореляційна функція ![]() .
.
Рішення. Користуючись тим, що ![]() нормально,
щільність імовірності другого порядку можемо представити у виді
нормально,
щільність імовірності другого порядку можемо представити у виді
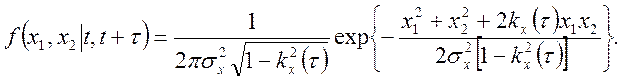
Шукане математичне чекання може бути представлене у виді
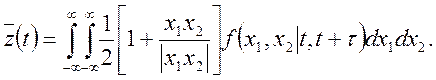
Тому що 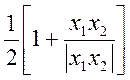 – тотожно дорівнює нулеві в тому випадку,
коли знаки в ординат х1 і х2 різні, і
дорівнює одиниці в протилежному випадку, те
– тотожно дорівнює нулеві в тому випадку,
коли знаки в ординат х1 і х2 різні, і
дорівнює одиниці в протилежному випадку, те
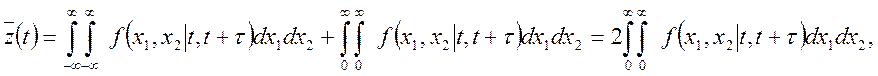
що після виконання інтегрування дає
результат, зазначений в умові задачі. (При інтегруванні зручно ввести нові
перемінні ![]() ,
, ![]() ,
поклавши
,
поклавши ![]() .)
.)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.