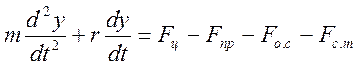Грубый и точный каналы регулирования частоты, страница 2

                    (2.1)

где m — масса подвижных частей, приведенная к координате перемещении тахометра; F_ц — сила, создаваемая центробежным тахометром; r — коэффи­циент вязкого трения; F_с.т— сила сухого трения; F_пр = F_np (у, l) — сила противодействующей пружины, зависящая от перемещения штока центро­бежного тахометра у и от перемещения основания поворотного рычага l; F_o.c=F_o.c —сила противодействующей пружины, связывающей золотник с рычагом обратной связи.

Сила, создаваемая центробежным тахометром,

                                                                       (2.2)

где m_г — масса грузов маятника; ρ — расстояние от центра тяжести грузов до оси  тахометра.                                                                                                     

Величина ρ может быть выражена через у, поэтому уравнение (2.2) можно записать в виде F_ц = F_ц (ω, у). Сила сухого трения F_с.т  незначительна и ею можно пренебречь, так как для ее уменьше­ния обойму золотника выполняют вращающейся. Исследования по­казывают, что силы инерции и вязкого трения малы, и в первом при­ближении ими также можно пренебречь, тогда уравнение (2.1) запишется

F_пр + F_о.с = F_ц                                                     (2.3)

В малых приращениях с учетом принятых направлений осей ко­ординат у, х, z (см. рис. 2.3) уравнение (2.3) примет вид:

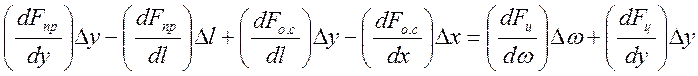
или

              (2.4)

где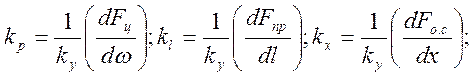   

.

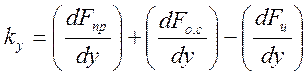Расход жидкости в единицу времени через серводвигатель про­порционален площади сечения, открываемого золотником в каналах гидроцилиндра, и квадратному корню из перепада давлений  в магистралях высокого и низкого давления:

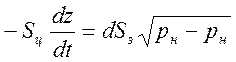                           (2.5)

где S_ц — площадь поршня сервомотора; S_з — площадь проходных отисрстнм золотника; d — коэффициент пропорциональности.

Допустим, что при малых перемещениях штока золотника пло­щадь проходных отверстий золотника S_з пропорциональна у, тогда уравнение (2.5) в малых приращениях принимает вид

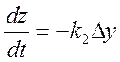,                                 (2.6)

где k₂ — коэффициент пропорциональности.

Как следует из уравнения (2.6), гидроцилиндр при принятых до­пущениях представляет собой интегрирующее звено.

С движением сервопоршня связано изменение угла дроссельной заслонки γ или угла наклонной шайбы. В малых приращениях связь между перемещением штока сервопоршня и управляющего элемента γ может быть записана как

Δγ = k₃Δz                                   (2.7)

где  k₃ — коэффициент  пропорциональности.

Связь между деформацией пружины Δx, вызванной действием жесткой обратной связи, и перемещением штока сервомотора Δz можно представить в виде

Δч = k₄Δz,                                 (2.8)

где k₄  - коэффициент   пропорциональности.

Разрешая уравнения (2.4), (2.6) — (2.8) относительно Δγ, по­лучим уравнение грубого канала регулирования частоты

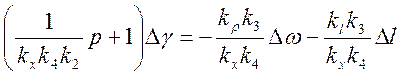                        (2.9)

В относительных приращениях уравнение (2.9) запишется так:

                          (2.10)

где Т_σ ≈ 1/k_xk₄k₂ — постоянная времени регулятора по грубому каналу; k_ν = k_νk₃ω_o/k_xk₄γ_o — коэффициент усиления грубого канала регулированиz чистоты вращения; k_ξ = k_ll_ok₃/k_xk₄γ_o— коэффициент передачи сигнала от корректора; γ = Δω/ω_o — относительное изменение угловой скорости; σ = Δγ/γ_o — относительное перемещение управляющего устройства привода; ξ = Δl/lo - относительное перемещение шайбы червячного редуктора корректора.