2. Найти, насколько быстро изменяется ошибка по мере изменения суммарного входа, получаемого выходным элементом. Эта величина (EI) равна произведению производной ошибки, полученной по формуле 3.4, на скорость изменения выхода элемента с изменением его суммарного входа.
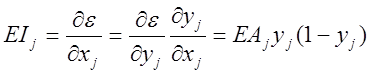(1.5)
3. Найти, с какой скоростью изменяется ошибка по мере изменения веса на входной связи выходного элемента. Эта величина (EW) равна произведению скорости изменения ошибки по мере изменения суммарного входа, получаемого выходным элементом, на уровень активности элемента, из которого исходит связь.
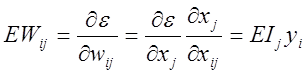(1.6)
4. Найти, как быстро изменяется ошибка с изменением активности элемента предыдущего слоя. Благодаря этому обратное распространение может быть применено к многослойным нейронным сетям. Изменение активности элемента предыдущего слоя оказывает влияние на активности всех выходных элементов, с которыми он связан. Следовательно, чтобы определить общее воздействие на величину ошибки, необходимо сложить все воздействия на выходные элементы. Эти воздействия будут равны произведению скорости изменения ошибки по мере изменения суммарного входа, получаемого выходным элементом, на вес связи к соответствующему выходному элементу.
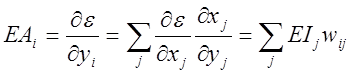(1.7)
Таким образом, с помощью шагов 2 и 4, можно преобразовать величины EA одного слоя элементов в EA предыдущего слоя. Эту процедуру необходимо повторять, чтобы вычислить EA всех слоев сети. А, зная EA элемента, можно, воспользовавшись шагами 2 и 3, найти EW на его выходных связях.
В работе [7] разработана математическая модель процесса нестационарного резания, которая для заданной толщины среза и переднего угла ставит в соответствие силу резания (рис. 3.1.). Эта математическая модель оказывается полезной для оптимизации станков и инструментов на этапе их проектирования. Однако в связи с тем, что для расчетов необходимо значительное время, оптимизация с помощью этой модели становится затруднительной.
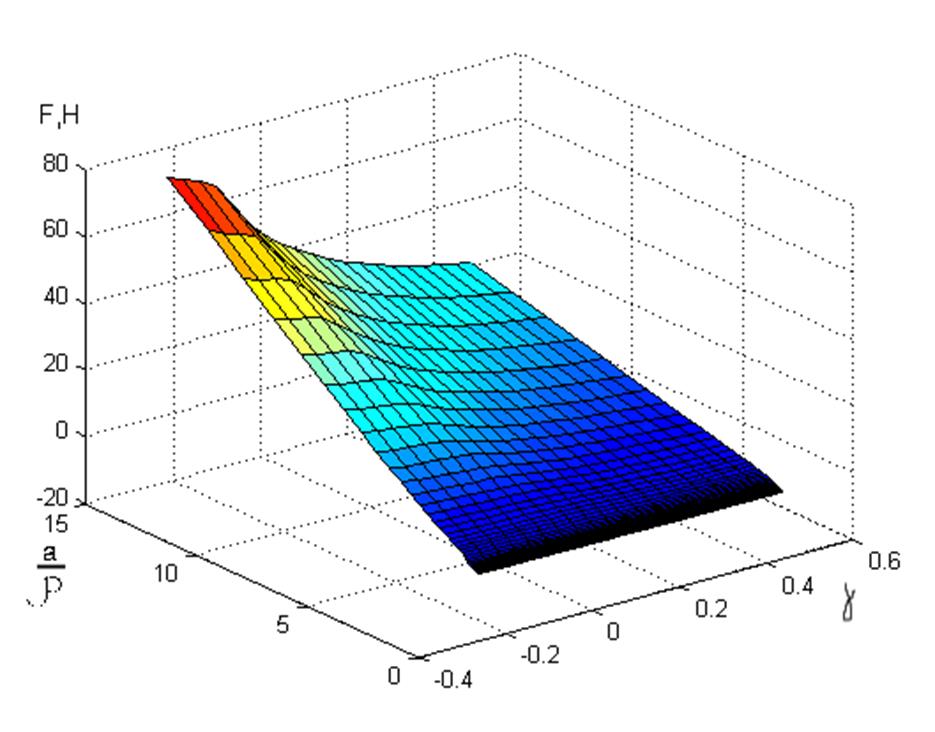Рис. 3.1. – Зависимость силы резания от
толщины среза и переднего угла.
Возможным решением является применение интерполяции для нахождения некоторых точек вместо их вычисления. Но интерполяция требует общего вида модели и неприемлема для случаев со многими переменными. Поэтому необходим другой подход, и одним из вариантов является использование нейронной сети. Нейронная сеть способна учитывать сколько угодно переменных почти без увеличения времени вычислений, и общий вид функции может быть любым.
Целью работы является разработка
методики, позволяющей существенно повысить скорость вычислений при применении
математической модели процесса нестационарного резания
, с целью снижения затрат времени на расчеты в процессе оптимизации.
.
Под построением
нейронной сети в данном случае подразумевается нахождение наиболее подходящей
для решения поставленной задачи структуры сети, т.е. вид сети, количество слоев
и нейронов в каждом из них. Осуществить выбор наиболее выгодной нейронной сети
возможно только экспериментальным путем. Поэтому было построено несколько сетей
и оценены погрешности получаемых с их помощью результатов. Исследовались
нейронные сети с одним и двумя скрытыми слоями. Сети обучалась с использованием
алгоритма обратного распространения. В качестве входных образов предъявлялись значения
толщины среза 
(в диапазоне от 0 до 14) и
переднего угла 
(в диапазоне от -0.2618 до
0.4363).
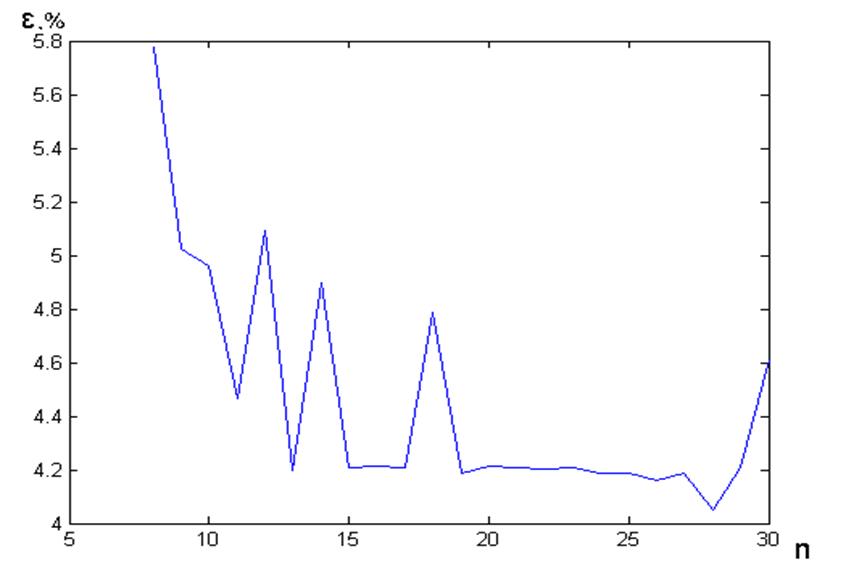
Рис. 3.2 – Погрешность результата, полученного с помощью однослойных нейронных сетей с количеством нейронов n, обученных на 1020
обучающих парах
Для нейронной сети с одним скрытым слоем погрешность результата оценивалась при количестве нейронов от 8 до 30, и различном количестве обучающих пар. При использовании 1020 обучающих пар (рис. 3.2) погрешность вычислений не превысила 6%, что является вполне удовлетворительным. При этом наилучшие результаты давали сети, состоящие из нейронов в количестве 13, от 15 до 17 и от 19 до 29.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.