Существуют два вида алгоритмов обучения: с учителем и без учителя. В случае обучения с учителем предполагается, что для каждого вектора входных образов существует так называемый целевой вектор – результат, который должен быть на выходе сети. Эти вектора, называемые обучающей парой, подаются сети одновременно. На основе входного вектора нейронная сеть вычисляет некоторый выход, который сравнивается с целевым вектором, разность – ошибка, допущенная сетью – с помощью обратной связи подается в сеть для использования ее при подстройке весов с целью минимизации ошибки. Настройка в соответствии с этой схемой ведется до тех пор, пока ошибка не достигнет допустимого уровня.
Другим способом настроить искусственную нейронную сеть является обучения без учителя. Этот способ более правдоподобен с точки зрения биологии, т. к. здесь обучающее множество состоит только лишь из входных векторов и сеть не нуждается в предъявлении заранее заготовленных ответов. В этом случае настройка сети проводится таким образом, чтобы достаточно близкие входные вектора давали одинаковые или близкие друг к другу выходные вектора. Процесс обучения, очевидно, выделяет статистические свойства обучающего множества и группирует сходные векторы в классы. Предъявление на вход вектора из некоторого класса даст определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет производиться этим классом входных векторов. Следовательно, выходы подобной сети должны трансформироваться в некоторую понятную форму, обусловленную процессом обучения. Это не является серьезной проблемой. Обычно не сложно идентифицировать связь между входом и выходом, установленную сетью.
Алгоритм обратного распространения (back propagation) играет ведущую роль в теории искусственных нейронных сетей. С его помощью возможно обучение сложных многослойных сетей, которые оказываются наиболее полезными на практике и значительно расширяют область применения нейрокомпьютинга.
Процедура обратного распространения является обучением с учителем. Таким образом, целью является подстройка весов так, чтобы расхождения между целевым и действительным выходным векторами сети уменьшились до некоторого допустимого уровня. Для этого необходимо, чтобы нейронная сеть вычисляла производную от ошибки по весам (EW), т. е. необходимо определить, как изменяется ошибка при изменении каждого веса.
Для описания алгоритма условимся, что элемент j – некоторый элемент выходного слоя, i – некоторый элемент, слоя предшествующего выходному. Функционирование сети при ее настройке с помощью обратного распространения условно делится на два этапа: проход вперед - стандартное вычисление выходных значений на основе входных, характерное для функционирования уже обученной нейронной сети; обратный проход – подстройка весов сети. Итак, на первом этапе вычисляется суммарный взвешенный вход xj с помощью формулы
,
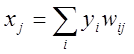(1.1)
где 
- уровень активности i–го элемента в предшествующем слое и 
-
вес связи между i–м и j–м элементами.
Затем вычисляется выходная активность 
с
использованием активационной функции вида
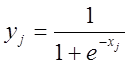(1.2)
Вторым этапом, после определения активностей
всех выходных элементов, сеть вычисляет ошибку 
, по
формуле
,
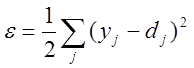(1.3)
где - уровень активности j-го элемента в верхнем слое, а 
- желаемый
выход j-го элемента.
Далее до получения приемлемого результата необходимо повторять четыре следующих шага:
1. Найти, насколько быстро меняется при изменении выходного элемента. Эта производная ошибки (EA) представляет собой разность между действительной и ожидаемой активностью.
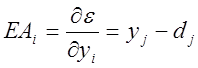(1.4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.