OUT = K(XW) (2.1),
где OUT – выходная активность, K - активационная функция, X – вектор входных сигналов, W – вектор весовых коэффициентов.
Т. о. поведение искусственной нейронной сети будет зависеть как от значений весовых коэффициентов, так и от активационной функции элементов сети. Обычно используется один из трех видов функций: линейная, пороговая или сигма-функция. Для линейных элементов выходная активность пропорциональна суммарному взвешенному входу. Для пороговых элементов выходная активность принимает одно из двух значений в зависимости от того, больше или меньше суммарный вход некоторого порогового значения. Для сигмоидальных элементов выход варьируется непрерывно и не линейно, по мере изменения входа. Сигмоидальные элементы имеют наибольшее сходство с реальными нейронами, к тому же сигмоидальная функция имеет вторую производную, которая используется в некоторых алгоритмах обучения сетей. Примером сигмоидальной функции может быть функция вида:
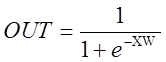 (2.2),
(2.2),
где X – вектор входных сигналов, W – вектор весовых коэффициентов.
Рассмотренная модель искусственного нейрона не учитывает многие свойства своего биологического прототипа. В частности в учет не берутся задержки во времени, которые оказывают влияние на динамику системы. Входные сигналы сразу же порождают выходной. Кроме того, не учитывается функция частотной модуляции или синхронизирующая функция биологического нейрона, которую многие ученые считают решающей.
 Каждый отдельный нейрон уже способен проводить
элементарные вычисления, но сила искусственных нейронов состоит в возможности
составления на их основе сложных сетевых парадигм, которые используются для
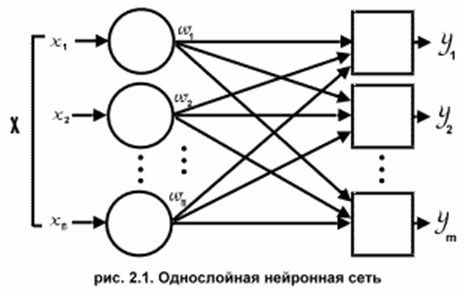
широкого круга задач. На рисунке 2.1 изображен простейший
вариант объединения нейронов в сеть. Вершины-круги слева служат для
распределения входного сигнала между нейронами сети. Они не выполняют
вычислений, и поэтому слоем их считать не будем. Вершины-квадраты составляют
слой искусственных нейронов, каждый из которых работает по описанной выше
схеме. Следует отметить, что рисунок описывает общий случай, тогда как в
действительности некоторые связи между нейронами могут отсутствовать. Также
могут иметь место связи между выходами и входами элементов в слое. Итак, в рассматриваемом случае, каждый элемент из множества
входов X соединен с каждым искусственным
нейроном, каждый из которых выдает на выход взвешенную сумму входов,
преобразованную с помощью активационной функции. Удобно считать веса связей элементами
матрицы W.Эта матрица имеет m столбцов и n строк,
где m – число входов,
а n – число нейронов. Например, w2,3 - это вес,
связывающий третий вход со вторым нейроном. Таким образом, получение выходного
вектора N, компонентами которого являются выходы OUT нейронов,
сводится к матричному умножению N = XW, где N и Х -
векторы-строки.
Каждый отдельный нейрон уже способен проводить
элементарные вычисления, но сила искусственных нейронов состоит в возможности
составления на их основе сложных сетевых парадигм, которые используются для
широкого круга задач. На рисунке 2.1 изображен простейший
вариант объединения нейронов в сеть. Вершины-круги слева служат для
распределения входного сигнала между нейронами сети. Они не выполняют
вычислений, и поэтому слоем их считать не будем. Вершины-квадраты составляют
слой искусственных нейронов, каждый из которых работает по описанной выше
схеме. Следует отметить, что рисунок описывает общий случай, тогда как в
действительности некоторые связи между нейронами могут отсутствовать. Также
могут иметь место связи между выходами и входами элементов в слое. Итак, в рассматриваемом случае, каждый элемент из множества
входов X соединен с каждым искусственным
нейроном, каждый из которых выдает на выход взвешенную сумму входов,
преобразованную с помощью активационной функции. Удобно считать веса связей элементами
матрицы W.Эта матрица имеет m столбцов и n строк,
где m – число входов,
а n – число нейронов. Например, w2,3 - это вес,
связывающий третий вход со вторым нейроном. Таким образом, получение выходного
вектора N, компонентами которого являются выходы OUT нейронов,
сводится к матричному умножению N = XW, где N и Х -
векторы-строки.
Аналогично строятся сети из искусственных нейронов с большим количеством слоев. В этом случае выход одного слоя является входом другого. Такие сети, как правило, обладают большей вычислительной мощностью.
Суть обучения сети заключается в настройке весов связей между нейронами, а иногда и структуры сети, таким образом, чтобы для некоторого множества входных образов сеть выдавала желаемое или хотя бы сходное с ним множество выходов. Обучение осуществляется путем последовательного предъявления входных образов с последующей подстройкой весов в соответствии с некоторым алгоритмом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.