






Значення оцінок ![]() ,
, ![]() . А шукана функція має вид
. А шукана функція має вид
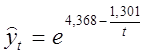 , t = 1, 2,
...,9. (1.56)
, t = 1, 2,
...,9. (1.56)
7 Припустимо, що моделююча функція ![]() тоді зв'язок між перемінними Y і t
будемо шукати у виді
тоді зв'язок між перемінними Y і t
будемо шукати у виді ![]() що
приводить до наступного перетвореній (лінійної)
моделі
що
приводить до наступного перетвореній (лінійної)
моделі ![]() Тепер
Тепер
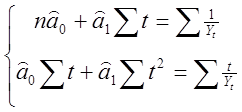 =>
=> 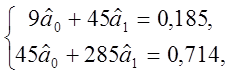
відкіля одержуємо ![]()
![]() тобто
тобто
![]() t = 1, 2, ..., 9.
(1.57)
t = 1, 2, ..., 9.
(1.57)
8 Якщо моделююча функція ![]() , то
думаємо
, то
думаємо ![]() И відповідно лінійна модель
И відповідно лінійна модель ![]() Далі, маємо
Далі, маємо
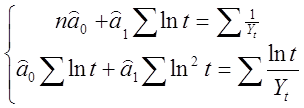 =>
=>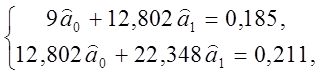
Отже, ![]()
![]() і
і
![]() t = 1, 2, ...,
9. (1.58)
t = 1, 2, ...,
9. (1.58)
9 В випадку ![]() чи
залежності
чи
залежності ![]() думаємо
думаємо ![]()
![]() Система нормальних рівнянь, що відповідає лінійної моделі, така:
Система нормальних рівнянь, що відповідає лінійної моделі, така:
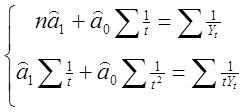 =>
=> 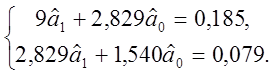
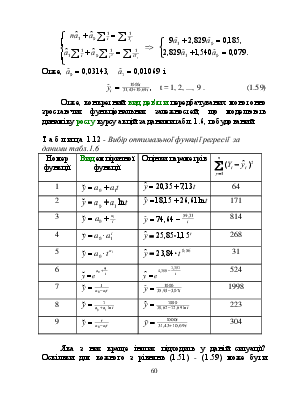
Отже, ![]()
![]() і
і
![]() t = 1, 2, ..., 9
. (1.59)
t = 1, 2, ..., 9
. (1.59)
Отже, конкретний вид дев'яти передбачуваних монотонно зростаючих функціональних залежностей, що моделюють динаміку росту курсу акцій за даними табл. 1.6, побудований.
|
Номер функції |
Вид емпіричної функції |
Оцінки параметрів |
|
|
1 |
|
|
64 |
|
2 |
|
|
171 |
|
3 |
|
|
814 |
|
4 |
|
|
268 |
|
5 |
|
|
31 |
|
6 |
|
|
524 |
|
7 |
|
|
1998 |
|
8 |
|
|
223 |
|
9 |
|
|
304 |
Яка з них краще інших підходить у даній ситуації? Оскільки для кожного з рівнянь (1.51) - (1.59) може бути обчислена сума квадратів відхилень значень, що спостерігаються, що пояснюється перемінної від теоретичних, тобто розрахованих по оціненому рівнянню регресії, те найбільш адекватному досліджуваному процесу будемо вважати ту, для якої ця сума найменша.
Аналіз результатів, представлених у
табл. 1.12, показує, що найбільш придатною оціненою функцією регресії при
моделюванні розглянутого процесу є статечна функція
![]() . Цілком задовільної
може бути і лінійна модель
. Цілком задовільної
може бути і лінійна модель ![]() . Видно також, що вибір
як модель гіперболічних функцій
. Видно також, що вибір
як модель гіперболічних функцій ![]() чи регресії
чи регресії ![]() є невдалим.
Зіставлення з результатами, приведеними в табл. 1.7, підтверджує в даному
випадку коректність критерію (1.33) при виборі оптимальної емпіричної функції
без знання чисельних значень оцінок параметрів моделей.
є невдалим.
Зіставлення з результатами, приведеними в табл. 1.7, підтверджує в даному
випадку коректність критерію (1.33) при виборі оптимальної емпіричної функції
без знання чисельних значень оцінок параметрів моделей.
1.7 Оцінювання параметрів функції податкових надходжень
В даний час гарно усвідомлюється той факт, що податкова система дуже впливає на розвиток народного господарства. Необґрунтовано завищений чи, навпаки, занижений рівень податкових відрахувань приводить до спаду виробництва, упадку бюджетної сфери й інших негативних наслідків. У цьому зв'язку слід зазначити, що недостатньо, наприклад, затверджувати, що сукупний податок повинний дорівнювати 40%. Потрібно ще вказати, до яких наслідків це чи приведе які показники будуть найкращими при 40%, і дати наукове обґрунтування цьому. Інакше виникає питання: чому саме 40%, а не 38% чи 21.6%, чи 58.14%?
Поставимо наступну задачу: які повинні бути податкові ставки, щоб загальні податкові надходження приймали найбільше значення. Вважаємо, що податкові ставки постійні для всіх товарів і послуг.
Очевидно, що при нульовій податковій ставці (H)
нало-говые надходження (Y) будуть
дорівнюють нулю. При стовідсотковій ставці всі оборотні кошти виробників
вилучаються, за-купка ресурсів стає неможливої, виробництво
останав-ливается, і податкові надходження різко
знижуються до нульового. Нехай ![]() - крива податкових
надходжень. Тоді
- крива податкових
надходжень. Тоді ![]() . З огляду на, що
. З огляду на, що ![]() при 0 < H < 1, заклю-чаем, що в деякій внутрішній крапці h* Î (0, 1) крива
при 0 < H < 1, заклю-чаем, що в деякій внутрішній крапці h* Î (0, 1) крива ![]() буде
приймати найбільше значення. Лаффер висунув гипо-тезу, що крива
буде
приймати найбільше значення. Лаффер висунув гипо-тезу, що крива ![]() має
один максимум і приблизно симетрична відносно прямої
H = h* поблизу крапки
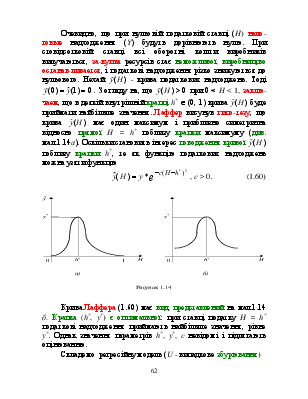
максимуму (див. мал.1.14а). Оскільки
становить інтерес поводження кривої
має
один максимум і приблизно симетрична відносно прямої
H = h* поблизу крапки
максимуму (див. мал.1.14а). Оскільки
становить інтерес поводження кривої ![]() поблизу крапки h*, те як функцію
податкових надходжень можна узяти функцію
поблизу крапки h*, те як функцію
податкових надходжень можна узяти функцію
|
|
![]() , c > 0.
(1.60)
, c > 0.
(1.60)
Крива Лаффера (1.60) має вид, представлений на мал.1.14 б. Крапка (h*, y*) є оптимальної: при ставці податку H = h* податкові надходження приймають найбільше значення, рівне y*. Однак значення параметрів h*, y*, c невідомі і підлягають оцінюванню.
Складемо регресійну модель (U - випадкове збурювання)
![]() , c > 0.
(1.61)
, c > 0.
(1.61)
Прологарифмировав, знаходимо
![]() .
.
Заміна
Z = ln, a = lny* - ch* 2, b = 2ch* (1.62)
дозволяє одержати параболічну регресію
Z = a + b - c2 + U, (1.63)
лінійну щодо оцінюваних параметрів і збурювання.
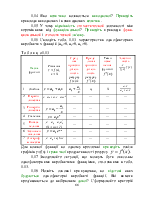
Система нормальних рівнянь (1.47) для визначення
оцінок ![]() ,
, ![]() ,
, ![]() параметрів a, b, c у
даному випадку здобуває вид
параметрів a, b, c у
даному випадку здобуває вид
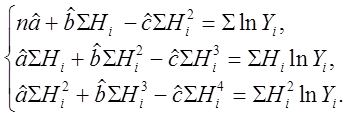 (1.64)
(1.64)
Якщо відомі значення ![]() ,
, ![]() ,
, ![]() , то, з
огляду на (1.62), знайдемо оцінки параметрів h*, y*.
Маємо
, то, з
огляду на (1.62), знайдемо оцінки параметрів h*, y*.
Маємо
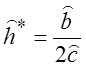 ,
, 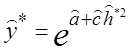 . (1.65)
. (1.65)
Отже, податкова політика держави при постійних
податкових ставках для всіх товарів і послуг була б обґрунтованої,
якщо ставка податку дорівнювала величині ![]() . У цьому випадку будуть досягатися
найбільші податкові поступ-ления в розмірі
. У цьому випадку будуть досягатися
найбільші податкові поступ-ления в розмірі ![]() .
.
Вправи
1.1 Функція витрат має вид
![]() .
.
При якому обсязі випуску xграничні витрати виробництва ![]() будуть
мінімальними?
будуть
мінімальними?
1.2 Установлено, що залежність фінансових нагромаджень підприємства від обсягу випуску виражається формулою
![]() .
.
Зробіть економічний аналіз функції фінансових нагромаджень.
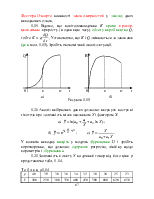
1.3 Знайдіть граничну продуктивність ресурсу (швидкість зміни випуску), якщо функція випуску має вид
![]() ,
,
а витрати ресурсу rскладають: а) 3 усл. ед.; б) 5 усл. ед. Визначите, починаючи з якого моменту збільшення витрат даного ресурсу стає економічно невигідним. Приведіть приклади економічних ситуацій, що можуть бути описані за допомогою функцій випуску зазначеного виду.
1.4 Цегельний завод робить x т цегли в день. Виробничі потужності заводу такі, що випуск цегли не може перевищувати 80т у день. За договором завод повинний поставити будівельній фірмі не менш 20т цегли в день. Визначите, при якому обсязі виробництва питомі витрати будуть найбільшими (найменшими), якщо функція витрат має вид
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.