Економетрика: Навчальний посібник (Оцінювання параметрів функції податкових надходжень), страница 2

 .

1.5  Підприємство робить x одиниць продукції на місяць і реалізує її за ціною

 .

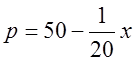Сумарні витрати виробництва складають

 .

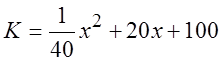Визначите, при якому обсязі виробництва прибуток підприємства буде максимальною.

1.6 Визначите швидкість зміни попиту (граничний попит) при ціні: а) 3 ден. ед.;   б) 5 ден. ед.; в) 7 ден. ед., якщо залежність попиту на товар від ціни виражається формулою

 .

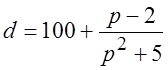1.7 Функція попиту на товар має вид

 .

Визначите рівні цін, що відповідають максимальному попиту на товар, зникненню попиту на нього. Чому дорівнює темп зміни попиту? Що це означає? Приведіть приклади ситуацій, що можуть бути описані за допомогою функцій попиту зазначеного виду.

1.8 Залежність попиту від ціни виражається формулою:

         а) ;                в) ;

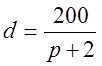         б) ;                   г) .

Опишіть динаміку зміни попиту на товар і виторги від продажу цього товару.

1.9 Нехай   - функція попиту,  - функція пропозиції. Знайдіть ціну равно-весия.  Чи є еластичними за ціною попит та пропозиція?

1.10 Формула  виражає залежність попиту від ціни. Визначите, при яких значеннях p попит еластичний, нееластичний, нейтральний. Як залежить виторг від зміни ціни? Зіставте з критеріями еластичності.

1.11 Відомо, що еластичність попиту на товар складає 0.6. Визначите, як зміниться доход від реалізації товару, якщо ціну на нього збільшити на 4%.

1.12 Установите залежність між показниками еластичності взаємно зворотних функцій у відповідних крапках. Відповідь: E₁E₂=1.

1.13 Установите залежність між показниками элас-тичности повних K і середніх  витрат виробництва. Відповідь: E_c=E_n-1.

1.14 Яка величина називається випадкової? Приведіть приклади випадкових і невипадкових величин.

1.15 У чому відмінність стохастической залежності між перемінними від функціональної? Приведіть приклади функ-циональной і стохастической зв'язку.

1.16 Складіть табл. 1.13 характеристик однофакторних виробничих функцій (a₀>0, a₁>0, a₂>0).

Т а б л и ц а 1.13

	Назва функції	Рівняння y = f (x), x > 0	Сред-няя произво-дитель-ность ресурсу f (x)/x	Преде-льная произво-дитель-ность ресурсу	Темп изме-нения функції	Эластич-ность
1	Лінійна			a1	0
2	Парабо-лическая		…	…	…	…
3	Гипербо-лическая		…	…	…	…
4	Статечна		…	…	…	…
5	Показа-тельная	(0 < a2 < 1)	…	…	…	…
6	Экспонен-циальная		…	…	…	…
7	Логариф-мическая		…	…	…	…

Для кожної функції на одному кресленні приведіть ескізи графіків y=f(x) і граничної продуктивності ресурсу  .

1.17 Змоделюйте ситуації, що можуть бути описа-ны однофакторними виробничими функціями, ста-ленними в табл. 1.13.

1.18 Назвіть основні припущення, на підставі яких будуються однофакторні виробничі функції. Які вимоги пред'являються до вибірковим даної? Сформулюйте критерій Фостера-Стюарта наявності законо-мерностей у зв'язку двох випадкових ознак.

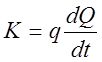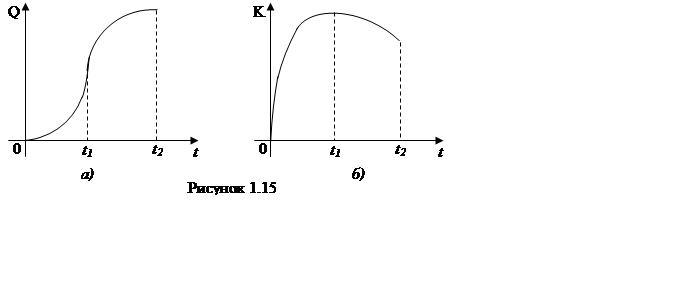
1.19 Відомо, що капіталовкладення K прямо пропор-циональны приросту (в одиницю часу) обсягу виробництва Q, тобто . Установлено, що K і Q змінюються за законами (див. мал. 1.15). Зробіть економічний аналіз ситуації.

 

1.20 Аналіз вибіркових даних дозволяє висунути наступні гіпотези про залежність між показником Y і фактором X:

а) ;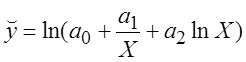

б) 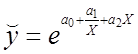;          в) .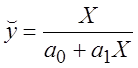

У кожнім випадку введіть у модель збурювання U і зробіть перетворення, що дозволяє одержати регресію, лінійну щодо параметрів і збурювання.

1.21 Залежність попиту Y на деякий товар від його ціни p представлена табл. 1.14.

Т а б л и ц а 1.14

p	40	39	38	36	34	32	30	26	25	23
Y	200	250	300	350	400	450	500	600	620	650

За допомогою критерію характерних середніх виберіть наилуч-шую функцію регресії з числа функцій, представлених у табл. 1.5.

1.22 Дайте геометричну інтерпретацію методу найменших квадратів оцінювання параметрів рівняння регресії. Геометрично поясните, чому МНК-оценки забезпечують мінімум суми квадратів відхилень.  Чи існує найбільше значення цієї суми?

1.23 Для перетворених моделей з 1.20 для деякого ряду спостережень складіть суму квадратів відхилень і запишіть системи нормальних рівнянь для одержання МНК-оценок невідомих параметрів. Якій додатковій умові в кожнім випадку повинний задовольняти ряд спостережень над X, щоб МНК-оценки існували?

1.24 Доведіть, що крапка характерних середніх  для функцій, представлених у табл. 1.5, лежить на соответству-ющей кривої регресії.

1.25 Складіть лінійну функцію регресії Y на p за даними табл. 1.14. Який очікуваний попит на товар буде при ціні: а) 28 усл. ед.; б) 22 усл. ед.?

1.26 У 80-і роки рівень дефіциту бюджету в США (Н.И.Коршунова, В.С.Танцюристів, 1996) складався в такий спосіб (табл. 1.15).

Т а б л и ц а 1.15 - Рівень дефіциту бюджету в США в 80-і роки (у % до вал. нац. продукту)

t	1980	1981	1982	1983	1984	1985	1986	1987	1988
Y	2,8	2,6	4,1	6,3	5,0	5,4	5,3	3,4	3,2

Досліджуйте характер зміни дефіциту бюджету в США, вважаючи, що він змінюється за законом

 ,

Знайдіть МНК-оценки  параметрів . Зробіть прогноз на 1989 р. і порівняєте його з оцінкою експертів, відповідно до якої дефіцит повинний скласти 3.2%.