Поиск преобразования Фурье и построение спектра заданной функции

Новосибирский государственный технический университет

Кафедра вычислительной техники

Расчетно – графическая работа

по дисциплине

«Кодирование»

Факультет:                  АВТ

Группа:                        АМ-015

Студент:                       Кивилев Д.С.

Преподаватель:          Титов Г.И.

Новосибирск, 2003

1. Найти преобразование Фурье и построить спектр функции f(t).

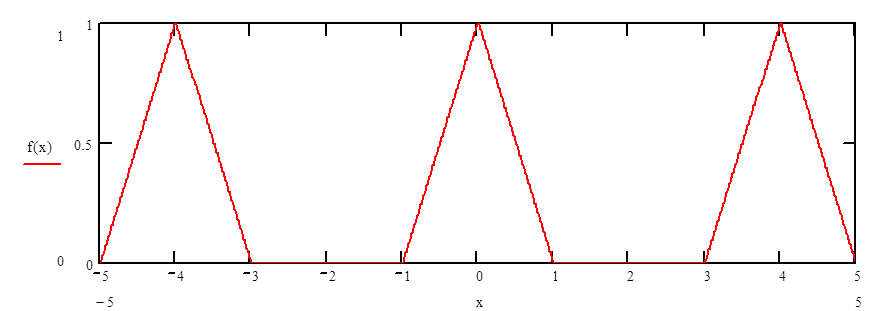
Рис. 1. Исходная функция

Функция заданная с помощью MathCad’a имеет следующий вид:

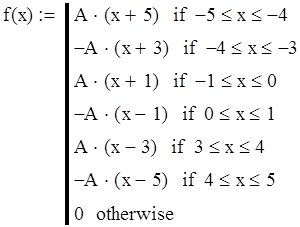
Применим к данной функции преобразование Фурье:

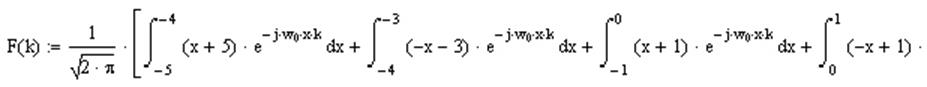
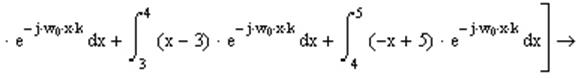
Результат полученный после извлечения интеграла:

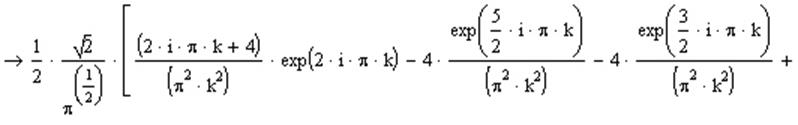
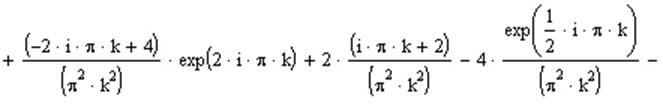
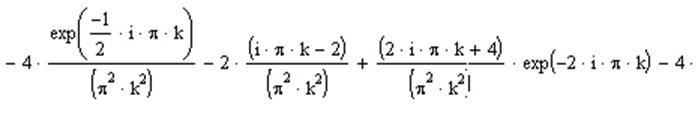
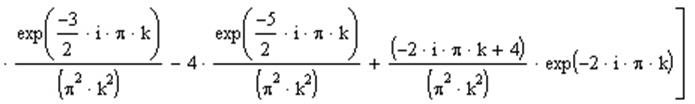
, где  .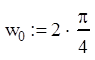

Далее, средствами всё того же MathCad’а, был построен график функции |F(k)| (рис. 2).

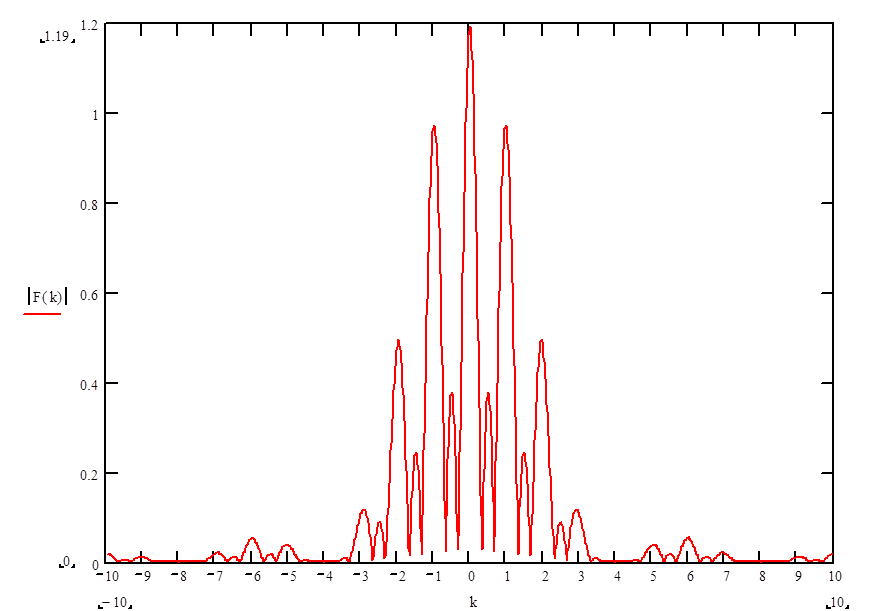
Рис. 2. Спектр исходной функции f(x)

2. Дополнить схему декодера циклического кода

Кодовая комбинация: 1001.

Схема: А, т.е. порождающий полином: = 1101.

Ошибка: в 7 разряде.

Определить:

1.  Что должна собой представлять ЛС, чтобы можно было исправлять однократные ошибки?

2.  Нужна ли ОС?

Для начала необходимо найти циклический код для заданного информационного слова (1001). Это делается путем дополнения информационного слова несколькими нулевыми битами (в данном случае тремя) и последующим делением на порождающий полином (1101).

	1	0	0	1	0	0	0		1	1	0	1
	1	1	0	1
		1	0	0	0
		1	1	0	1
			1	0	1	0
			1	1	0	1
				1	1	1	0
				1	1	0	1
				=	0	1	1

Таким образом, остаток от деления = 011.

Далее необходимо записать передаваемое слово: А_пер = 1001 011.

Декодер:

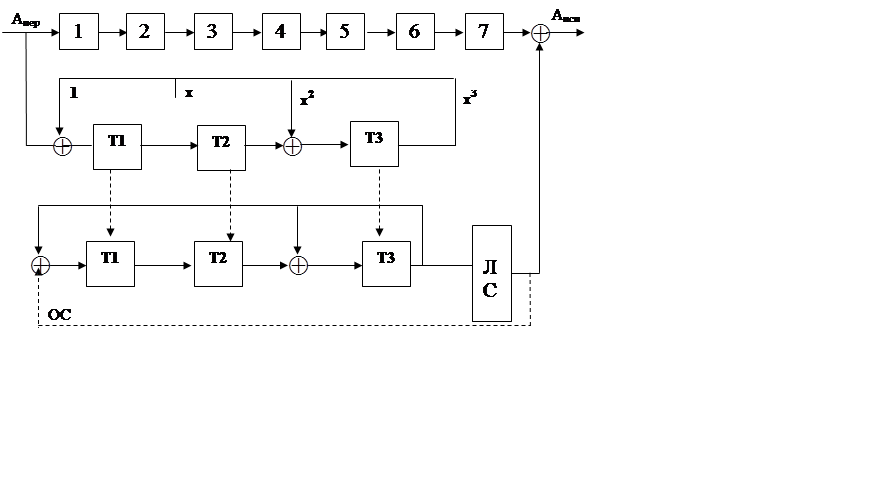Рис. 3. Схема декодера с неизвестной логической схемой исправления

Принцип работы декодера может быть описан следующими выражениями:

, , .

, , .

Теперь  необходимо проанализировать работу схемы в различных ситуациях: без ошибки и с ошибками, и исходя из полученных результатов выбрать комбинационную схему.

Такт	Регистр задержки							Т1	Т2	Т3	Т’1	Т’2	Т’3
-	1	2	3	4	5	6	7	0	0	0
1	1							1	0	0
2	0	1						0	1	0
3	0	0	1					0	0	1
4	1	0	0	1				0	0	1
5	0	1	0	0	1			1	0	1
6	1	0	1	0	0	1		0	1	1
7	1	1	0	1	0	0	1	0	0	0
8		1	1	0	1	0	0				0	0	0
9			1	1	0	1	0				0	0	0
10				1	1	0	1				0	0	0
11					1	1	0				0	0	0
12						1	1				0	0	0
13							1				0	0	0
Табл. 1. Работа схемы без ошибки