Поиск преобразования Фурье и построение спектра заданной функции, страница 2

А_{пер с ошибкой} = 1001 010

Из табл.1 видно, что когда код без ошибки, то на седьмом такте в триггерах нижней схемы получаем нули. Из таблицы 2 видно, что когда есть однократные ошибки, то в том такте, в котором на выходе появляется ошибочный разряд, в триггерах нижней схемы содержится комбинация 011. Исходя из этого вид логической схемы (ЛС) будет следующим:

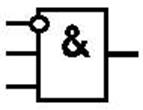
Рис. 4. Вид логической схемы

В данном случае обратная связь нужна. С её помощью при формировании единичного корректирующего бита происходит обнуление триггеров T’1, T’2 и T’3.

Однако, без ОС можно было и обойтись, т.к. полученный во время выхода ошибочного бита код 011 является уникальным и в других тактах не повторяется, следовательно, корректирующий бит будет сформирован только в момент возникновения ошибки.

3. Выводы

В ходе выполнения РГР были успешно решены все поставленные задачи. Конечно,

нахождение спектра функции осуществлено мат. методами, а не теми формальными или же методами предстваления исходной функции другими функциями. Опять же без MathCad’a пришлось бы очень не просто.

            Во втором задании логическая схема исправления ошибок будет одинакова для данной схемы декодера, т.е. при порождающем полиноме , при всех одиночных ошибках.