Числовые ряды, страница 4

Доказательство:

Рассмотрим частичные суммы с четными номерами:  разности во всех скобках неотрицательны, поэтому  – возрастающая последовательность. С другой стороны,   поэтому , т.к. все разности в скобках неотрицательны. Ограниченная возрастающая последовательность имеет конечный предел, т.е.  причем

Рассмотрим предел последовательности частичных сумм с нечетными номерами:

 т.е. и частичные суммы с нечетными номерами имеют тот же предел, т.е. ряд сходится, а т.к.  и их предел не превосходит по абсолютной величине модуля первого члена ряда.

Пример:  Этот ряд не является абсолютно сходящимся, т.к.  - гармонический ряд. Однако, условия теоремы Лейбница выполняются: 1) 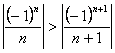 и  поэтому ряд сходится (сходимость условная)

Замечание: Если условие 1) выполняется, начиная с какого-то номера в последовательности членов, то вывод о сходимости ряда сохраняется, а оценка модуля суммы ряда модулем первого члена ряда не имеет места.

Следствие: если остаток ряда удовлетворяет условиям теоремы Лейбница, то при замене ряда частичной суммой погрешность не превзойдет абсолютной величины первого отброшенного члена.

Замечание: Абсолютно сходящиеся ряды сходятся к одной и той же сумме, как бы произвольно не переставлены были члены ряда, т.е. ведут себя так же, как конечные суммы.

Условно сходящийся ряд перестановкой членов ряда можно заставить сходится к любому наперед заданному числу или расходиться.