Числовые ряды, страница 2

Необходимое условие сходимости ряда

Теорема: Если ряд сходится, то предел его общего члена равен нулю.

Доказательство:

Расходимость гармонического ряда:

Гармонический ряд: . Необходимое условие сходимости  выполнено, однако  Каждая из скобок превосходит  потому частичные суммы неограниченно растут т.е. ряд расходится.

Стало быть, если сходится, то  но из того, что  не следует сходимость ряда.

Следствие: Если  то ряд расходится.

Примеры: 1)  расходится, т.к.   

2)  расходится, т.к.  (можно применить правило Лопиталя, получим)

 Ряд называют знакоположительным, если все его члены больше нуля, и знакоотрицательным, если все члены меньше нуля.

Знакоположительные и знакоотрицательные ряды называют знакопостоянными рядами. Если среди членов ряда конечное число членов имеет один знак, например, минус, а остальные члены другой знак, например, плюс, то отбросив частичную сумму, содержащую все слагаемые со знаком минус получим остаток ряда с положительными членами, т.к. остаток ряда определяет, сходится или расходится ряд, ряды с конечным числом членов одного знака можно рассматривать как знакопостоянные.

Знакопеременные ряды – ряды, содержащие бесконечное число как положительных, так и отрицательных слагаемых.

В знакопостоянных рядах последовательность частичных сумм монотонна, поэтому для сходимости ряда достаточна ограниченность последовательности частичных сумм.

Достаточные признаки сходимости для знакопостоянных рядов

Не ограничивая общности (см. свойство 1 для сходящихся рядов), будем формулировать признаки для знакопостоянных рядов.

Первый признак сравнения:

Пусть для членов рядов  и  выполнено условие:  (вообще говоря, для всех  начиная с какого-то номера, см. следствие из свойства 3 сходимости рядов), тогда:

а) если ряд с большими членами сходится, то и ряд с меньшими членами сходится;

б) если ряд с меньшими членами расходится, то и ряд с большими членами расходится.

Доказательство:

а) Если ряд  сходится, то его частичные суммы возрастают и ограничены  но частичные суммы ряда  возрастают и не превосходят частичных сумм ряда , т.е. тоже ограничены, поэтому ряд  сходится.

б) Если расходится, то его возрастающие частичные суммы должны стремиться в  тогда и частичные суммы ряда  неограниченно возрастают.

Теорема доказана.

Примеры:

1)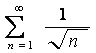 расходится т.к. , а  - гармонический расходящийся ряд;