2) ![]() сходится, т.к.
сходится, т.к. ![]() а ряд
а ряд ![]() сходится
(см. пример 4) в начале лекции).
сходится
(см. пример 4) в начале лекции).
Второй признак сравнения (предельный)
Даны два ряда: ![]() и
и ![]()
Если существует конечный,
отличный от нуля предел отношения общих членов этих рядов: ![]() то ряды либо оба сходятся, либо оба
расходятся, при этом говорят, что члены у этих рядов одинакового порядка.
то ряды либо оба сходятся, либо оба
расходятся, при этом говорят, что члены у этих рядов одинакового порядка.
Пример:
![]() сходится,
т.к. его можно сравнить со сходящимся рядом
сходится,
т.к. его можно сравнить со сходящимся рядом ![]()
![]()
Признак Даламбера
Если существует конечный
предел отношения последующего члена ряда к предыдущему: ![]() ,
то если
,
то если ![]() ряд расходится, если
ряд расходится, если ![]() ряд сходится, если
ряд сходится, если ![]() нужны дополнительные исследования
сходимости ряда.
нужны дополнительные исследования
сходимости ряда.
Примеры: 1) ![]() сходится, т.к.
сходится, т.к. ![]()
2) ![]() расходится, т.к.
расходится, т.к. ![]()
3) Гармонический ряд ![]() расходится, а
расходится, а 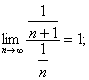
4) ![]() сходится, а
сходится, а ![]()
Замечание: признак Даламбера удобен, когда члены ряда содержат показательную функцию или n-факториал. Если член ряда есть дробно-степенная функция, признак Даламбера не решает вопрос о поведении ряда.
Интегральный признак сходимости рядов:
Ряд ![]() и
и 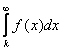 (при
(при
![]() на
на ![]() одновременно
сходится или расходится.
одновременно
сходится или расходится.
Этот признак может быть
использован для вывода о сходимости рядов ![]() при
при
![]() ряд сходится,
ряд сходится, ![]() ряд расходится. Поведение
соответствующих интегралов рассмотрено в теме «несобственные интегралы».
ряд расходится. Поведение
соответствующих интегралов рассмотрено в теме «несобственные интегралы».
Ряды знакопостоянные сходятся, если их члены достаточно быстро стремятся к нулю.
Знакопеременные ряды могут сходиться не благодаря быстрому стремлению членов ряда к нулю, а из-за того, что последовательность частных сумм не является монотонной.
Если ряд сходится, и ряд из модулей членов ряда тоже сходится, то ряд называют абсолютно сходящимся.
Если ряд сходится, а ряд из модулей членов ряда расходится, то ряд называют условно сходящимся.
Условно сходиться могут только знакопеременные ряды.
Теорема: Если ряд из модулей членов ряда сходится, то и сам ряд сходится.
В доказательстве используют первый признак сравнения.
Из знакопеременных рядов рассмотрим знакочередующиеся ряды, т.е. такие ряды, у которых любые два соседних члена имеют разные знаки. Для таких рядов есть достаточное условие сходимости.
Теорема Лейбница
Если в знакочередующемся
ряде ![]() выполняются два условия: 1) члены
ряда убывают по абсолютной величине
выполняются два условия: 1) члены
ряда убывают по абсолютной величине ![]() . 2) предел общего
члена равен нулю
. 2) предел общего
члена равен нулю ![]() , то ряд сходится, и модуль
суммы этого ряда не превосходит модуля первого члена.
, то ряд сходится, и модуль
суммы этого ряда не превосходит модуля первого члена.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.